Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 11
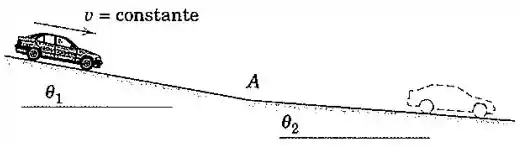
Um carro está descendo a encosta de inclinação com os freios ligeiramente acionados de modo que a velocidade é constante. A inclinação diminui bruscamente para no ponto . Se o condutor não muda a força de frenagem, determine a aceleração do carro após este passar no ponto . Avalie a sua expressão para e .
Passo 1
Inicialmente, o carro está em equilíbrio, pois sua velocidade é constante. Então, se analisarmos as forças na direção de descida (direção do vetor ), precisamos que essas forças se anulem. E quais são essas forças?
Bom, temos a força de frenagem, no sentido contrário ao da velocidade, que permanecerá com seu módulo constante depois do ponto .
E também temos uma componente da força peso, no mesmo sentido da velocidade, cujo módulo será:
Então, a equação que representa o equilíbrio entre essas forças é:
Assim obtivemos uma expressão para .
Passo 2
Quando o carro passar do ponto , a força continuará a agir sobre o carro, no sentido contrário ao da nova velocidade, que segue a inclinação de .
Nessa mesma direção, mas no mesmo sentido da nova velocidade, teremos um novo valor da componente da força peso, dado por:
A Segunda Lei de Newton nos dá:
Substituímos as expressões já obtidas de e :
Obtivemos então a expressão de . Agora vamos avaliá-la para e :