Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 109
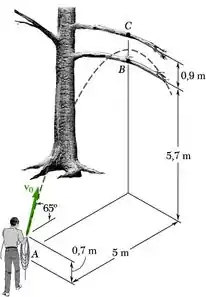
Enquanto segura uma das extremidades, o trabalhador lança um rolo de corda sobre o galho mais baixo da árvore. Se ele joga a corda com uma velocidade inicial v0 a um ângulo de 65° com a horizontal, determine a variação de valores de v0 para que a corda passe apenas sobre o galho mais baixo.
Passo 1
E aí galera tudo bem ? O enunciado pede que a gente encontre a variação de valores de v0 para que a corda passe apenas sobre o galho mais baixo.
Passo 2
Movimento horizontal. (Uniforme)
Em qualquer B ou C, x = 5 m
Passo 3
Movimento vertical. (Movimento uniformemente acelerado)
Nos galhos da árvore, t = tBC
Passo 4
No ponto B:
ou
No ponto C:
Resposta
Exercícios de Livros Relacionados
Determine o raio de curvatura da trajetória descrita pela partícula do Problema 11.95 quando t = 0.
Uma partícula se move ao longo da espiral mostrada na figura. Determine a intensidade da velocidade da partícula em termos de b, θ , θ ˙ .
Uma partícula se move ao longo da espiral mostrada na figura. Determine a intensidade da velocidade da partícula em termos de b, θ , θ ˙ .
Determine a direção da binormal à trajetória descrita pela partícula do Problema 11.96 quando (a) t = 0, (b) t = π /2 s.
Mostre que r ˙ = h ϕ ˙ sen θ sabendo que, para o instante mostrado na figura, o degrau AB do aparelho de ginástica está girando no sentido anti-horário a uma taxa constante ϕ ˙ .