Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 106

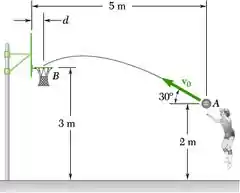
Uma jogadora de basquete arremessa a bola a 5 m da tabela. Sabendo que a bola tem uma velocidade inicial v0 em um ângulo de 30° com a horizontal, determine o valor de v0 quando d é igual a (a) 0,2 m e (b) 0,38 m.

Passo 1

E ai galera tudo beleza? O exercício pede que a gente determine o valor de v0 quando d é igual a (a) 0,2 m e (b) 0,38 m.

Primeira nota

v 0 x = v 0 cos ⁡ 30 °

v 0 y = v 0 sin ⁡ 30 °

Passo 2

Movimento horizontal. (Uniforme)

x = 0 v x 0 t

Em B:

5 - d = v 0 cos ⁡ 30 ° t             ou             t B = 5 - d v 0 cos ⁡ 30 °

Passo 3

Movimento vertical. (Movimento uniformemente acelerado)

y = y 0 + v y 0 t - 1 2 g t 2             g = 9,81   m / s 2

Em B:

y = 3

y 0 = 2

3 - 2 = v 0 sin ⁡ 30 ° t B - 1 2 g t B 2

Substituindo para t B

1 = v 0 sin ⁡ 30 ° 5 - d v 0 cos ⁡ 30 ° - 1 2 g 5 - d v 0 cos ⁡ 30 ° 2

Rearranjando:

1 = tan ⁡ 30 ( 5 - d ) - 1 2 g 5 - d v 0 cos ⁡ 30 ° 2

1 2 g 5 - d v 0 cos ⁡ 30 ° 2 = tan ⁡ 30 5 - d - 1

v 0 2 = g 2 × 5 - d 2 cos 2 ⁡ 30 × [ 5 - d × tan ⁡ 30 - 1 ]

v 0 = g 2 × 5 - d cos ⁡ 30 5 - d × tan ⁡ 30 - 1

Passo 4

  1. d = 0,2 m.:

    2. v 0 = 9,8 2 × 5 - 0,2 cos ⁡ 30 5 - 0,2 × tan ⁡ 30 - 1 = 9,22   m / s

    Passo 5

  2. d =0,38

v 0 = 9,8 2 × 5 - 0 38 cos ⁡ 30 5 - 0 , 38 × tan ⁡ 30 - 1 = 9 , 15   m / s

Resposta

a )   v 0 = 9,22   m /s

b )   v 0 = 9,15   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a hélice cônica do Problema 11.95, determine o ângulo que o plano de oscilação forma com o eixo y.
O movimento de uma partícula sobre a superfície de um cilindro circular reto é definido pelas relações R = A, 2 π t e z = At2/4, onde A é uma constante. Determine as intensidades da velocidade e da ac
O movimento tridimensional de uma partícula é definido por suas coordenadas cilíndricas (veja a Fig. 11.26) R = A/(t + 1), θ = Bt e z = Ct/(t + 1). Determine as intensidades da velocidade e da acelera
Como o motorista de um automóvel viaja para o norte a 25 km/h em um estacionamento, ele observa um caminhão aproximando pelo noroeste. Depois ele reduz sua velocidade escalar para 15 km/h e assim que
O bloco C parte do repouso em t = 0 e move-se para cima com aceleração constante de 25 mm/s2. Sabendo que o bloco A move-se para baixo com velocidade constante de 75 mm/s, determine (a) o instante no