Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 12
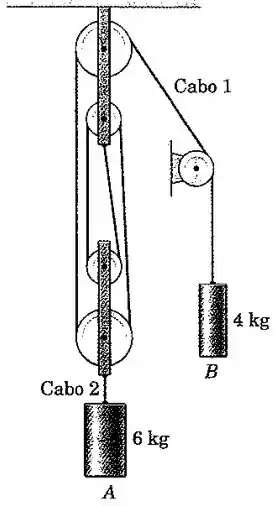
A talha é liberada a partir do repouso com todos os cabos esticados. Despreze o atrito e a massa de todas as polias e determine a aceleração de cada cilindro e as trações e nos dois cabos.
Passo 1
Galera, vamos escrever primeira a equação da Segunda Lei de Newton para o cilindro :
Para escrever a Segunda Lei de Newton para o cilindro , uma coisa importante que sempre devemos lembrar quando trabalhamos com problemas de corda sem massa é que a tração é sempre a mesma em toda a corda. Sendo assim, há “pedaços” de corda que indiretamente puxam , e cada um desse pedaços também vão fazem uma força de tração para cima, olha só:
Passo 2
Porém, ainda temos somente duas equações e três incógnitas, ou seja, precisamos de mais uma equação.
Uma dica: quando já escrevemos todas as equações da Segunda Lei de Newton e ainda há mais incógnitas do que equações, isso geralmente se resolve procurando alguma relação entre as acelerações, por meio da geometria do problema.
Nesse caso, podemos notar que, a cada vez que o cilindro sobe um comprimento , então o cilindro desce um comprimento , pois é como se cada “pedaço” da corda se movimentasse , o que resulta num movimento total da corda de . Escrevemos assim:
O sinal negativo é devido a um estar subindo enquanto o outro desce. Derivando essa equação duas vezes em relação ao tempo, encontramos:
Agora sim temos um sistema de três equações e três incógnitas:
Passo 3
Resolvendo o sistema, com , obtemos:
Já a tração podemos calcular usando a Segunda Lei de Newton para o cilindro , pois já sabemos a aceleração dele:
Lembre-se que as trações e só deram valores diferentes porque elas não são aplicadas na mesma corda, beleza?