Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 108

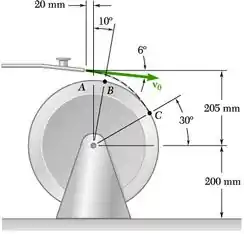
O bocal em A descarrega água de refrigeração com uma velocidade inicial v0 a um ângulo de 6° com a horizontal sobre um esmeril de 350 mm de diâmetro. Determine o intervalo de valores da velocidade inicial para o qual a água vai cair no esmeril entre os pontos B e C.

Passo 1

E ai galera tudo certo? O enunciado pede que a gente encontre o intervalo de valores da velocidade inicial para o qual a água vai cair no esmeril entre os pontos B e C.

v x 0 = v 0 cos ⁡ 6 °

v y 0 = - v 0 sin ⁡ 6 °

Passo 2

Movimento horizontal. (Uniforme)

x = 0 v x 0 t

Movimento vertical. (Movimento uniformemente acelerado)

y = y 0 + v y 0 t - 1 2 g t 2             g = 9.81   m/ s 2

No ponto B:

x = 0.175   m sin ⁡ 10 °

x = 0.175   m cos ⁡ 10 °

x :             0.175 sin ⁡ 10 ° = - 0.020 + v 0 cos ⁡ 6 ° t

t B = 0.050388 v 0 cos ⁡ 6 °

y :             0.175 cos ⁡ 10 ° = 0.205 + v 0 sin ⁡ 6 ° t B - 1 2 g t B 2

Passo 3

Substituindo por tB

- 0.032659 = - v 0 sin ⁡ 6 ° 0.050388 v 0 cos ⁡ 6 ° - 1 2 9.81 0.050388 v 0 cos ⁡ 6 ° 2

v 0 2 = 1 2 9.81 0.050388 2 cos 2   6 ° 0.032659 - 0.050388 tan ⁡ 6 °

v 0 B = 0.678   m/s

Passo 4

No ponto C:

x = 0.175   m cos ⁡ 30 °

y = 0.175   m sin ⁡ 30 °

x :             0.175 cos ⁡ 30 ° = - 0.020 + v 0 cos ⁡ 6 ° t

t C = 0.171554 v 0 cos ⁡ 6 °

y :             0.175 sin ⁡ 30 ° = 0.205 + - v 0 sin ⁡ 6 ° t C - 1 2 g t C 2

Passo 5

Substituindo por tC

- 0.117500 = - v 0 sin ⁡ 6 ° 0.171554 v 0 cos ⁡ 6 ° - 1 2 9.81 0.171554 v 0 cos ⁡ 6 ° 2

v 0 2 = 1 2 9.81 0.171554 2 cos 2   6 ° 0.117500 - 0.171554 tan ⁡ 6 °

v 0 C = 1.211   m/s

Resposta

0.678   m/s ≤ v 0 ≤ 1.211   m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de basquete é solta no chão no ponto A e quica com velocidade vA de intensidade 2,25 m/s como mostrado na figura. Determine o raio de curvatura da trajetória descrita pela bola (a) no ponto A
Os carros de corrida A e B se deslocam em trechos circulares de um autódromo. No instante mostrado na figura, a velocidade de A está decrescendo a uma taxa de 7 m/s² e a velocidade de B está aumentand
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0 que forma um ângulo α com a horizontal. Expresse o raio de curvatura da trajetória do projétil no ponto C em termos de x, v0,
O carvão é descarregado da carroceria de um caminhão basculante com uma velocidade inicial de vA = 2 m/s ∡ 50°. Determine o raio de curvatura da trajetória descrita pelo carvão (a) no ponto A, (b) no
Uma partícula se move ao longo da espiral mostrada na figura. Determine a intensidade da velocidade da partícula em termos de b, θ , θ ˙ .