Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 249
Na talha diferencial mostrada, as duas polias superiores estão presas uma na outra para formar uma só unidade. O cabo é enrolado em torno da polia menor com sua extremidade fixada na polia de modo que este não possa escorregar. Determine a aceleração acendente do cilindro se o cilindro tem uma aceleração descendente de . (Sugestão: Analise geometricamente as consequências de um movimento diferencial do cilindro ).
Passo 1
Vamos seguir a sugestão do enunciado: pensar em termos de movimentos diferenciais, e usando o método de “semelhança de triângulos” que o livro emprega.
As polias de (Polia ) e (Polia ) se movem juntas, mas como o raio da segunda é do raio da primeira, podemos definir a seguinte relação:
Vamos desenhar isso:
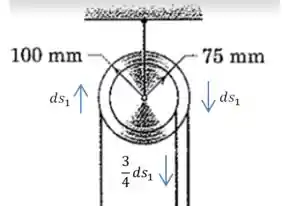
Passo 2
Como essas duas cordas à esquerda da figura estão ligadas na polia lá de baixo, e nosso objetivo é definir qual o deslocamento do centro dessa polia quando acontece:
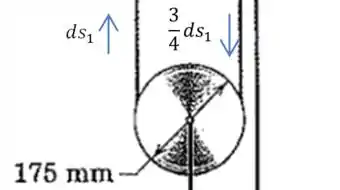
E é aqui que entra o método do livro, vamos representar esses deslocamentos da seguinte forma:
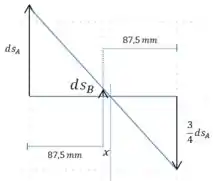
Agoravamos tentar usar semelhança de triângulos para achar :
Podemos cortar o , e então:
E agora que sabemos , podemos usar a semelhança para achar :
Passo 3
E como sempre temos que lembrar após resolver questões de polias pelo método da inspeção: a proporção entre os deslocamentos se mantém para as acelerações:
Isso pode ser demonstrado derivando em relação ao tempo. Então:
Resposta
A aceleração ascendente do cilindro é de