Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 58
Determine o tempo para o satélite completar a sua órbita em torno da Terra. A órbita tem um raio r medido a partir do centro da Terra. As massas do satélite e da Terra são e , respectivamente.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Além disto, precisamos relembrar como se calcula a força gravitacional entre dois corpos. Ela é dada por:
Utilizando estas duas relações, conseguiremos determinar a velocidade do satélite. Como ela é constante, para descobrirmos qual é o tempo necessário para dar uma volta, basta relembrarmos as primeiras equações aprendidas da cinemática e calcular:
Vamos a questão então!
Passo 2
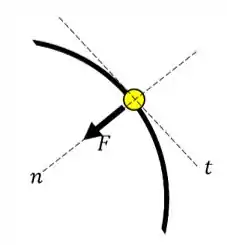
Considerando o satélite uma partícula, podemos esboçar o seu diagrama de corpo livre. No plano dado pela direção normal e tangencial, o mesmo está sujeito apenas a ação da força gravitacional na direção normal. Portanto, temos o seguinte diagrama.
Passo 3
Conforme pode ser visualizado no diagrama de corpo livre esboçado no passo anterior, o satélite está sujeito apenas a ação da força gravitacional na direção normal. Como ele possui uma trajetória circular, ele está sujeito a uma aceleração centrípeta.
Portanto, vamos fazer o somatório de forças nesta direção. Obtemos então:
Passo 4
Agora, só nos falta calcular o tempo para o satélite dar uma volta ao redor da Terra. Utilizando a relação do Passo 1, temos: