Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 37
Resolva o Problema 18.32 usando a equação de conservação de energia.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O problema 18.32 pede para determinarmos a velocidade angular da barra no instante .
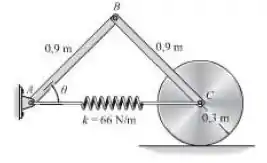
Sabemos que as duas barras finas têm e o disco tem . A mola não está deformada quando e o disco rola sem deslizar.
Agora vamos aplicar conservação de energia:
Passo 2
No primeiro momento o sistema está em repouso e a mola não está deformada, portanto e . Considerando sempre os centros de massa, temos:
Sabemos que:
Portanto:
Como , temos:
Resposta
Exercícios de Livros Relacionados
Um colar de 500 g pode deslizar sem atrito sobre uma barra curva BC em um plano horizontal. Sabendo que o comprimento indeformado da mola é de 80 mm e que k = 400 kN/m, determine (a) a velocidade que
Uma barra circular delgada é sustentada em um plano vertical por um suporte em A. Uma mola de constante k = 45 N/m e comprimento indeformado igual ao arco de círculo AB está presa ao suporte e enrolad
Uma barra circular delgada é sustentada em um plano vertical por um suporte em A. Uma mola de constante k = 45 N/m e comprimento indeformado igual ao arco de círculo AB está presa ao suporte e enrolad
O sistema mostrado na figura está em equilíbrio quando 0. Sabendo que inicialmente ϕ = 90 ° e que o bloco C está em movimento suave e muito lento quando o sistema está naquela posição, determine a vel
Um bloco de 300 g é liberado do repouso em A e desliza sem atrito ao longo da superfície mostrada na figura. Determine a força exercida sobre o bloco pela superfície (a) justamente antes de o bloco al