Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 73
A haste do magnetômetro de uma nave espacial é constituída por um grande número de unidades com formato triangular que emergem para sua configuração de operação após a liberação a partir do recipiente em que foram dobradas e embaladas antes da liberação. Escreva uma expressão para a força que a base do recipiente deve exercer sobre a haste durante a sua instalação em termos do comprimento crescente e suas derivadas no tempo. A massa da haste por unidade do comprimento instalado é . Considere a base de suporte sobre a nave espacial como uma plataforma fixa e assuma que a instalação ocorre fora de qualquer campo gravitacional. Despreze a dimensão comparada com .
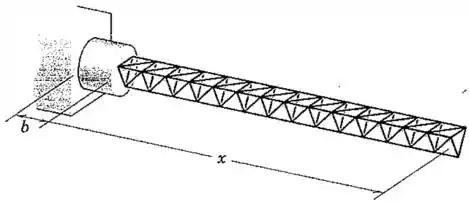
Passo 1
Como a instalação ocorre fora de qualquer campo gravitacional, a única força externa agindo sobre a haste é a exercidade pela base, que vamos chamar de , então:
Como a densidade linear da haste é , podemos representar a massa em função do comprimento como:
E então a taxa de variação da massa:
E a “velocidade” do sistema é simplesmente a taxa com que o comprimento aumenta:
E a aceleração é a taxa com que essa velocidade aumenta:
Passo 2
Substituindo isso na fórmula, temos:
Resolvido!
Resposta
A força exercida pela base deve ser .