Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 45

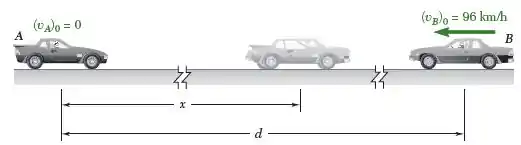
O carro A está estacionado ao longo da posta na direção norte de uma rodovia e o carro B está viajando na pista e direção sul a uma velocidade constante de 96 k m / h . Em t = 0 , A liga o motor e acelera a uma taxa constante a A ,   enquanto em t = 5 s , B começa a diminuir a velocidade com uma desaceleração constante de intensidade a A / 6 . Sabendo que quando os carros se cruzam x = 88 m   e   v A = v B , determine (a) a aceleração a A , (b) quando os veículos se cruzam, (c) a distancia d entre os veículos quando t = 0 .

Passo 1

Para t ≥ 0 : v A = 0 + a A t x A = 0 + 0 + 1 2 a A t ²

0 ≤ t < 5 : x B = 0 + ( v B ) 0 t ( v B ) 0 = 60 m i / h = 88 f t / s

Em t = 5 s : x B = ( 88 f t / s )   x   ( 5 s ) = 440 f t

Para t ≥ 5 s : v B = v B 0 + a B   x   t - s a B = - 1 6 a A

x B = x B s + v B 0   x   t - s + 1 2 a B   x   t - s ²

Presumir t > 5 s quando os carros passam um pelo o outro.

Naquela hora t A B ,

v A = v B :   a A t A B = ( 88 f t / s ) - a A 6   x   ( t A B - 5 )

x A = 295 f t : 294 f t = 1 2 a A t A B 2

Passo 2

Então a A   x   ( 7 6 t A B - 5 6 ) 1 2 a A t A B 2 = 88 294

Ou 44 t A B 2 - 343 t A B + 245 = 0

Resolvendo t A B = 0,795 s     e     t A B = 7,00 s

  1. Com t A B > 5 s , 294 f t = 1 2 a A   x   ( 7,00 s ) ²
  2. De cima

    3. Nota: uma solução aceitável não pode ser encontrada se for assumido que t A B ≤ 5 s .

  3. Temos: d = x + x B t A B = 294 f t + [ 440 f t + ( 88 f t / s )   x   7,00 s s

+ 1 2   x   - 1 6   x 12,00 f t s 2   x   7,00 s ² s ²

Resposta

  1. a A = 12,00 f t / s ²
  2. t A B = 7,00 s
  3. d = 906 f t
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula está se movendo ao longo de uma linha reta de tal maneira que a sua aceleração é definida como a = - 2 vm / s 2 , onde v é dado em metros por segundo. Se v = 20m / s quando s=0 e t=0, de
Um caminhão está viajando ao longo de uma linha reta com uma velocidade descrita pelo gráfico. Construa o gráfico a-s para 0
O gráfico a - s para um jipe viajando ao longo de uma estrada reta é dado para os primeiros 300 m desse movimento. Construa o gráfico v - s . Em s = 0 , v = 0 .
Um carro sobe uma encosta com a velocidade mostrada. Determine a distância total que o carro percorre até ele parar (t = 60s). Elabore um gráfico a - t .
O trenó motorizado desloca-se ao longo de um curso reto de acordo com o gráfico v-t. Construa os gráficos s - t e a - t para o mesmo intervalo de tempo de 50 s. Quando t=0 , s=0 .