Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 53
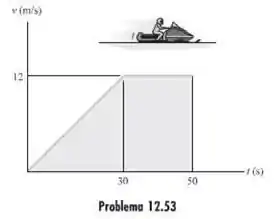
O trenó motorizado desloca-se ao longo de um curso reto de acordo com o gráfico v-t. Construa os gráficos e para o mesmo intervalo de tempo de s. Quando , .
Passo 1
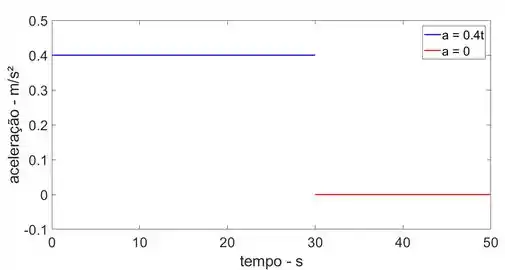
Gráfico : Utilizando é possível encontrar as curvas de aceleração para os dois intervalos mostrados.
Para o intervalo 0
Para t = 30 m,
Para o intervalo 30
Para t = 50 m,
Passo 2
A aceleração pode ser obtida em termos do tempo e da velocidade, fazendo a = dv/dt.
Para o intervalo 0
Para o intervalo 30
Resposta
O gráfico está mostrado abaixo.
Exercícios de Livros Relacionados
Uma tubulação horizontal descarrega no ponto A um jato de água dentro de um reservatório. Determine o raio de curvatura do jato no ponto B em termos das intensidades das velocidades vA e vB.
Em um dado instante de uma corrida de aeronaves, o avião A está voando horizontalmente em linha reta e sua velocidade escalar aumentada a uma taxa de 8 m/s2 . O avião B está voando na mesma altitude q
Uma bola de basquete é solta no chão no ponto A e quica com velocidade vA de intensidade 2,25 m/s como mostrado na figura. Determine o raio de curvatura da trajetória descrita pela bola (a) no ponto A
Os carros de corrida A e B se deslocam em trechos circulares de um autódromo. No instante mostrado na figura, a velocidade de A está decrescendo a uma taxa de 7 m/s² e a velocidade de B está aumentand
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0 que forma um ângulo α com a horizontal. Expresse o raio de curvatura da trajetória do projétil no ponto C em termos de x, v0,