Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 139
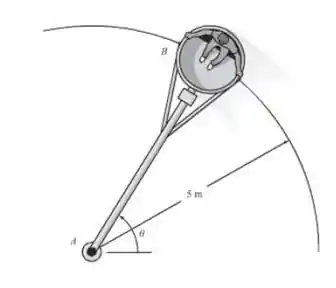
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de , onde é dado em segundos. Se um carro parte do repouso quando , determine as intensidades da sua velocidade e aceleração quando . Despreze a dimensão do carro.
Passo 1
Está questão é bem simples! Como a aceleração tangencial foi dada em função da o tempo , basta integrarmos uma vez para obtermos a função da velocidade! Depois, é só substituir o valor final de t, o qual é . Com o valor da velocidade, temos todos os parâmetros necessários para calcularmos as componentes tangencial e normal da aceleração, utilizando as equações da cinemática que estamos bastante acostumados!
Passo 2
Vamos obter as funções da velocidade e da posição. Para isto, vamos começar integrando a função da aceleração tangencial.
Portanto, quando , temos:
Passo 3
Agora, para calcularmos as componentes da aceleração, podemos substituir os valores diretamente nas suas equações. Começando pelo termo tangencial, temos:
Já para a componente normal, temos:
Portanto, calculando a intensidade da aceleração, temos: