Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 29

Um motorista dirigindo um automóvel sobre um declive com 8% de inclinação efetua uma frenagem abrupta e "patina" por uma distância de 30 m antes de colidir com um carro estacionado. Um advogado contrata um especialista que mede o coeficiente de atrito cinético entre os pneus e a pista, obtendo um valor de μ k = 0,45 . O advogado está correto ao acusar o motorista de ter excedido o limite de velocidade de 25 mph (40,23 km/h)? Explique.

Passo 1

E aí galera, vamos iniciar mais uma questão do nosso livro!

Primeiramente vamos anotar alguns dados importantes fornecido na questão:

d i s t â n c i a   d e   d e r r a p a g e m = d = 30   m

μ k = 0,45

Em seguida vamos desenhar o problema para visualizá-lo. Isso nos ajudará a resolvê-lo facilmente.

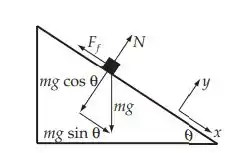
O ângulo é:

θ = tan - 1 ⁡ 0,08 = 4 ° 34 '

As equações do movimento são:

Para o eixo y :

F N = m g cos ⁡ θ  

Para o eixo x :

m x ¨ = m g sin ⁡ θ - F f

Desde que:

F f = μ k F N = μ k m g cos ⁡ θ

Desta forma:

x ¨ = g sin ⁡ θ - μ k g cos ⁡ θ

Integrando esta equação, obtemos:

x ˙ = g t sin ⁡ θ - μ k cos ⁡ θ + x ˙ i

Onde x ˙ i é a velocidade inicial.

Integrando a equação da velocidade, obtemos:

x = 1 2 g t 2 sin ⁡ θ - μ k cos ⁡ θ + x ˙ i t + x i

Agora, precisamos encontrar o tempo necessário para parar quando a velocidade inicial é:

v i = 25 M P H = 11,2   m / s  

Então:

x ˙ = g t sin ⁡ θ - μ k cos ⁡ θ + x ˙ i

0 = g t sin ⁡ θ - μ k cos ⁡ θ + 11,2

t = 11,2 g sin ⁡ θ - μ k cos ⁡ θ

= 3,1   s

Portanto, o automóvel parará depois de percorrer uma distância:

x = 1 2 g t 2 sin ⁡ θ - μ k cos ⁡ θ + x ˙ i t + x i

x - x i = 1 2 ( 9,8 ) 3,1 2 sin ⁡ θ - μ k cos ⁡ θ + 11,2 × 3,1

= 17,35  

O motorista estava em alta velocidade porque se ele estivesse indo a 25 MPH ele não iria bater no carro.

Finalizamos aqui nossa questão, tudo beleza? Te vejo na próxima!

Resposta

O   a d v o g a d o   e s t a v a   c o r r e t o   a o   a c u s a r   o   m o t o r i s t a

Exercícios de Livros Relacionados

Cada um dos blocos A e B tem massa m. Determine a maior força horizontal P que pode ser aplicada a B de maneira que A não se desloque em relação a B. Todas as superfícies são lisas.
No tubo de raios catódicos, elétrons tendo massa m são emitidos de um ponto-fonte S e começam a se mover horizontalmente com uma velocidade inicial v 0 . Quando passam entre as placas-grade em uma dis
Cada um dos blocos A e B tem massa m. Determine a maior força horizontal P que pode ser aplicada a B de maneira que A não se desloque em relação a B. O coeficiente de atrito estático entre A e B é μ s
Se uma força horizontal de P = 50N é aplicada ao bloco A determine a aceleração do bloco B. Despreze o atrito. Dica: mostre que a B = a A tg ⁡ 15 °
O anel C de 1 kg ajusta-se livremente no eixo liso. Se a mola está livre quando s = 0 e ao anel é dada uma velocidade de 4,5m / s , determine a velocidade do anel quando s = 0,3m .