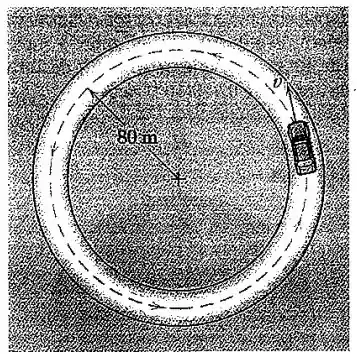
Um carro de teste parte do repouso em uma pista horizontal circular de 80m de raio e aumenta sua velocidade a uma taxa uniforme para atingir os 100k m / h em 10 segundos. Determine o módulo a da aceleração total do carro 8 segundos após a partida.

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 101

Um carro de teste parte do repouso em uma pista horizontal circular de de raio e aumenta sua velocidade a uma taxa uniforme para atingir os em segundos. Determine o módulo da aceleração total do carro segundos após a partida.

Passo 1

Galera, a primeira coisa a se fazer aqui é calcular a componente tangencial da aceleração, dada por:

Como a taxa de variação da velocidade é constante, podemos escrever assim:

Lembre-se que :

Passo 2

Agora vamos calcular a aceleração normal, lembrando que no caso do movimento circular, ela é dada por:

onde é o módulo da velocidade e é o raio do círculo.

Então, como queremos a aceleração quando , precisamos calcular nesse mesmo instante. Como a aceleração tangencial é constante, podemos escrever assim:

Desse modo, substituindo esse valor de e o raio , temos a aceleração normal:

Passo 3

Show! Já temos as componentes tangencial e normal da aceleração. Então o módulo da aceleração total será dado por:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/118)No projeto de um mecanismo de temporização , o movimento do pino A na ranhura circular fixa é controlado pela guia B , que está sendo elevado por seu parafuso de acionamento com uma velocidade c

2/121) O projeto preliminar de uma “pequena”estação espacial para orbitar a terra em uma trajetória circular consiste em um anel (toro) com uma seção transversal circular como mostrado . O espaço habi

2/120) A roda e a polia acoplada giram sobre o eixo fixo em O e são acionadas pela correia mostrada . Em um determinado instante a velocidade e a aceleração de um ponto A sobre a correia são 0,6 m / s

2/117) Para simular uma condição de “ausência de peso”na sua cabine , um avião de transporte a jato viajando a 800 k m / h se desloca continuamente em umacurva vertical como mostrado . A que taxa β '

2/124) Uma pequena partícula P parte do ponto O com uma velocidade desprezível e aumenta sua velocidade para umvalor v = 2 g y , onde y é a altura vertical a partir de O . Quando x = 15m , determine a