Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 59
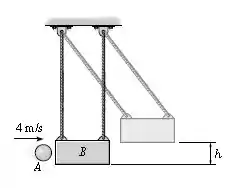
A bola de é lançada até o bloco suspenso de a uma velocidade de . Se o coeficiente de restituição entre a bola e o bloco é , determine a altura máxima até onde o bloco balançará antes de parar momentaneamente.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando conservação de quantidade de movimento, temos:
Substituindo os valores, temos:
O coeficiente de restituição é dado por:
Substituindo os valores, temos:
Resolvendo o sistema, temos:
Aplicando a conservação de energia, temos:
Resposta
Exercícios de Livros Relacionados
Quando a corda está a um ângulo de α=30 ° a esferaAde 1 kg tem uma velocidadev0= 0,6 m/s. O coeficiente de restituição entreAe cunhaBde 2 kg é 0,8 e o comprimento da cordal= 1 m. A constante da mola t
Os blocos A e B têm massa de 0,5 kg cada, e o bloco C de 1,5 kg. O coeficiente de atrito entre os blocos e o plano é k =0,30. Inicialmente, o bloco A move-se a uma velocidade vo= 4 m/s e os blocos B e
Uma bolaBde 70 g é largada de uma alturah0= 1,5 m e alcança uma alturah2= 0,25 m após dois quiques em placas idênticas de 210 g.AplacaArepousa diretamente no chão duro, ao passo que a placaCrepousa so
Quando a corda está a um ângulo de α=30 ° , a esferaAde 0,5 kg tem uma velocidadev0= 1,2 m/s. O coeficiente de restituição entreAe cunhaBde 0,9 kg é 0,7 e o comprimento da cordal= 0,8 m. A constante d
O raio da órbita da lua de um determinado planeta é igual a duas vezes o raio desse planeta. Denotando por p a densidade média do planeta, mostra que o tempo necessário para a lua completar uma revolu