Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 203
O carro está viajando na velocidade constante de enquanto contorna a curva circular com de raio e no instante representado está na posição . O carro está viajando na velocidade constante de e passa pelo centro do círculo neste mesmo instante. O carro é localizado em relação ao carro pelas coordenadas polares e com o pólo se deslocando com . Para esse instante determine e os valores de e conforme medidos por um observador no carro .
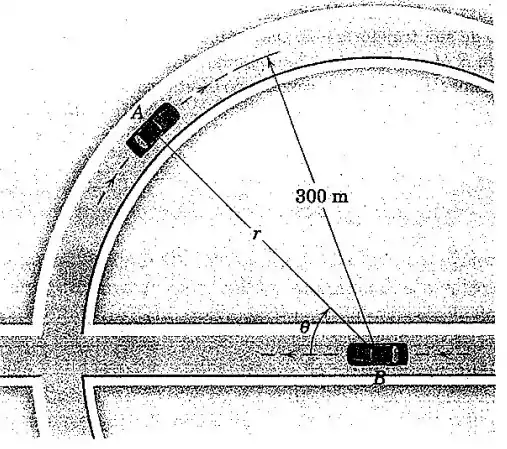
Passo 1
Sejam e as velocidades em módulo dos carros e , respectivamente. Considerando o eixo positivo para a direita, o eixo positivo para cima e a origem no centro, temos:
A velocidade relativa será então dada por:
E o módulo dela será:
Passo 2
A mesma velocidade também pode ser escrita em coordenadas polares, assim:
onde será o vetor unitário na direção da distância e será o vetor unitário girado de no sentido anti-horário a partir de . Então podemos decompor e em coordenadas retangulares assim:
Logo, podemos reescrever a velocidade assim:
Como já sabemos que , vamos substituir de uma vez:
Passo 3
Agora vamos igualar a expressão de que acabamos de encontrar ao seu valor que já conhecíamos:
Igualando componente a componente, resulta num sistema de duas equações e duas incógnitas:
cuja solução é:
Se considerarmos o sentido de aumento do ângulo como a seta indica na figura, oposto ao que usamos em nossos cálculos, obteremos: