Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 71
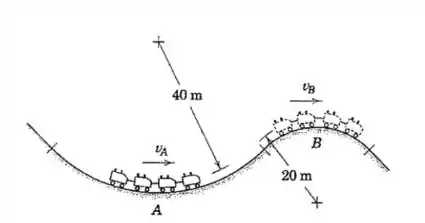
Os carros de uma atração de parque de diversões têm uma velocidade em e uma velocidade em . Se um passageiro de se senta sobre uma balança de mola (que registra a força normal exercida sobre esta), determine a leitura da balança quando o carro passa pelos pontos e . Suponha que os braços e as pernas da pessoa não sustentam uma força considerável.
Passo 1
Bom pessoal, a gente sabe que quando um corpo está realizando um movimento circular, existe necessariamente uma força centrípeta atuando sobre ele, certo? Essa força sempre aponta para o centro da trajetória. No caso dessa questão, a situação é a seguinte:
Se os carros estivessem andando no plano, a força normal estaria simplesmente se cancelando com o peso dos carros, mas quando o carro está em uma trajetória circular nós sabemos que essas duas forças não estão se cancelando: elas formam uma resultante centrípeta.
Passo 2
Vamos lembrar da expressão para força centrípeta:
A gente sabe que, tanto no ponto quanto no ponto , essa força é a resultante entre a normal e o peso, certo?
Vamos dizer que o sentido positivo é vertical para cima. Nesse caso:
E então as forças normais, em cada um dos casos, vão ser:
Passo 3
E agora é só substituir os valores numéricos:
E para o caso :
Pronto!
Resposta
A balança registra no ponto e no ponto .