Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 64
3/64) Calcule a velocidade rotacional necessária para a atração aérea de um parque de diversões a fim de que os braços das gôndolas assumas um ângulo com a vertical . Despreze a massa dos braços aos quais as gôndolas estão presas e trate cada gôndola como uma partícula .
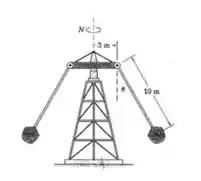
Passo 1
Bom pessoal , para resolvermos este exercício temos que aplicar o princípio do somatório das forças concorrentes na direção normal à trajetória e na direção do eixo .
Na direção normal à trajetória , temos que :
Na direção do eixo , por sua vez :
Passo 2
Então galera , dividindo a equação (1) por (2) , obtemos que :
Sendo assim ,
Para acharmos a velocidade angular em , basta aplicarmos a fórmula :
Resposta
E aí , topa fazer mais exercícios com a gente?
Exercícios de Livros Relacionados
Uma bola de massa m é guiada ao longo da trajetória circular vertical r = 2 r c cos θ usando o braço O A . Se o braço tem velocidade angular constante θ ˙ 0 determine o ângulo θ ≤ 45 ° no qual a bol
Um garoto parado firmemente em pé gira a garota sentada em um ‘prato’ circular ou trenó em uma trajetória circular de raio r 0 = 3 m de tal maneira que sua velocidade angular é θ ˙ 0 = 0,1 rad/s. Se o
A partícula lisa tem massa de 80 g. Ela está ligada a uma corda elástica estendendo-se de O a P e, devido ao braço de guia ranhurado, desloca-se ao longo da trajetória circular na horizontal r = 0,8 s
O cilindro C de 1,5 kg desloca-se ao longo da trajetória descrita por r = ( 0,6 sen θ ) m. Se o braço está girando O A no sentido anti-horário com uma velocidade angular de θ ˙ = 3 rad/s, determine
O tubo gira no plano horizontal com uma taxa constante de θ ˙ = 4r a d / s . Se a bola B de 0,2 kg parte da origem O com uma velocidade radial inicial de r ˙ = 1,5m / s e se movimenta para fora do tub