Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 171

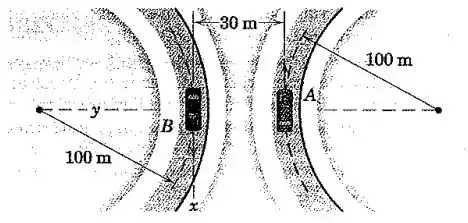
Os carros A e B estão contornando as curvas com velocidades iguais 72 km/h. Determine a velocidade que A parece ter para um observador se deslocando e girando com o carro B para o instante representado. A curvatura da estrada para o carro A afeta o resultado? Os eixos x-y estão fixados no carro B.

Passo 1

Bom galera, é muito importante destacar que essa questão foca apenas na velocidade dos carros. Então, vamos fazer um esquema indicando esses vetores.

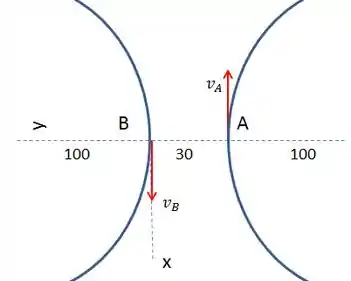
Vamos agora usar a equação da velocidade relativa entre os pontos A e B.

v A = v B + ω × r A B + v r e l

Como a referência é o ponto B, ω tem com base em sua trajetória. Então:

ω = 72 3,6 × 100 = 0,2   k ^ r a d / s

Pessoal, outra coisa: temos que prestar atenção nos eixos x-y da questão, pois eles estão em posições diferentes do habitual. Substituindo os dados na equação:

- 20 i ^ = 20 i ^ + 0,2 k ^ × - 30 j ^ + v r e l

- 40 i ^ - 6 i ^ = v r e l

v r e l = - 46 i ^   m / s

Então, já resolvemos a questão e percebemos que a trajetória curva de A não teve nenhuma influência com o resultado.

Resposta

v r e l = - 46 i ^   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o instante representado, a barra CB está girando no sentido anti-horário a uma taxa constante N = 4r a d / s , e seu pino A provoca uma rotação sentido horário do membro ranhurado ODE. Determine
O cursor montado sobre molas oscila no eixo de acordo com x = 0,04 s e n π t , onde x é expresso em metros e t é expresso em segundos. Simultaneamente a estrutura gira em torno do mancal em O com uma
O guindaste gira em torno do eixo z com uma taxa constante ω 1 = 0,6r a d / s , enquanto a lança gira para baixo com uma taxa constante ω 2 = 0,2r a d / s . Determine a velocidade e aceleração do pont
O guindaste gira em torno do eixo z com uma taxa de ω 1 = 0,6r a d / s , a qual está aumentando em ω ˙ 1 = 0,6r a d / s 2 . Além disso, a lança gira para baixo a ω 2 = 0,2r a d / s , a qual está aumen
O motor gira em torno do eixo z com uma velocidade angular constante ω 1 = 3r a d / s . Simultaneamente, o eixo O A gira com uma velocidade angular constante ω 2 = 6r a d / s . Além disso, o anel C de