Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 144

O corpo apresentado é construído de uma haste esbelta uniforme e consiste em um anel de raio r fixado a uma seção reta de comprimento 2 r . O corpo se articula livremente em relação a uma junta esférica em O . Se o corpo está em repouso na posição vertical mostrada e recebe um leve empurrão, calcule a sua velocidade angular ω após uma rotação de 90 ° em torno (a) do eixo A - A e (b) do eixo B - B .

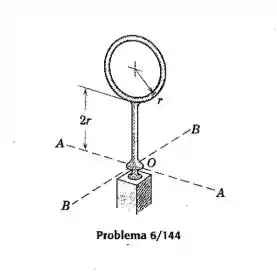
Passo 1

Para acharmos a posição y do centro de massa do conjunto, fazemos

y - = ∑ r m ∑ m

Podemos considerar a grandeza ρ (massa por unidade de comprimento) como

ρ = m l

Para a haste temos m h   e para o anel m a

m h = 2 ρ r     e m a = ρ 2 π r

Retomando a equação para o centro de massa do conjunto,

y - = 2 ρ r r + 2 π ρ r 3 r 2 ρ r ( 1 + π )

Por fim,

y - = r 1 + 3 π 1 + π

Passo 2

Em torno do eixo A-A, temos

I A - A = 1 3 2 ρ r 2 r 2 + 1 2 ( 2 π ρ r ) r 2 +   2 π ρ r ( 3 r ) ²

De onde tiramos que

I A - A = r ² m 18 + 57 π 6 ( 1 + π )

Passo 3

Em torno do eixo B-B, temos

I B - B = 1 3 2 ρ r 2 r 2 + ( 2 π ρ r ) r 2 +   2 π ρ r ( 3 r ) ²

De onde tiramos que

I B - B = r ² m 4 + 30 π 3 ( 1 + π )

Resposta

I A - A = r ² m 18 + 57 π 6 ( 1 + π )

I B - B = r ² m 4 + 30 π 3 ( 1 + π )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema mostrado na figura consiste de um colar A de 20 kg e um contrapeso B de 10 kg e está em repouso quando uma força constante de 450 N é aplicada ao colar A. (a) Determine a velocidade de A exa
Um bloco de 3 kg repousa sobre um bloco de 2 kg que está apoiado, mas não preso, a uma mola de constante 40 N/m. O bloco superior é subitamente removido. Determine (a) a velocidade máxima alcançada pe
O sistema mostrado na figura está em repouso quando uma força constante de 150 N é aplicada em um colar B. (a) Se a força atua por meio de todo movimento, determine a velocidade do colar B que atinge
Um bloco de 3 kg repousa sobre um bloco de 2 kg, que está preso a uma mola de constante 40 N/m. O bloco superior é subitamente removido. Determine (a) a velocidade máxima alcançada pelo bloco de 2 kg,
Os blocos A e B têm massas de 11 kg e 5 kg, respectivamente, e estão a uma altura h = 2 m acima do chão, quando o sistema é liberado do repouso. Exatamente antes de atingir o chão, o bloco A está se m