Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 177

O cursor montado sobre molas oscila no eixo de acordo com x = 0,04 s e n π t , onde x é expresso em metros e t é expresso em segundos. Simultaneamente a estrutura gira em torno do mancal em O com uma velocidade angular ω = 2 s e n π t 2 r a d / s . Determine a aceleração do centro C do cursor (a) quando t = 3 s e (b) quando t = ½ s.

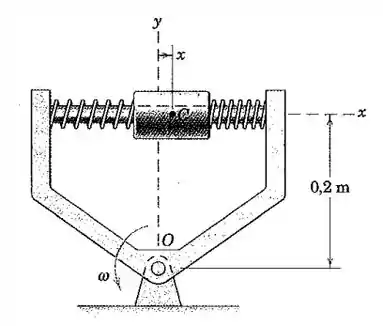
Passo 1

Bom pessoal, o esquema está representado de modo mais simples abaixo.

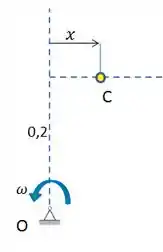
Agora, sabendo a expressão de movimento do cursor C, podemos achar sua velocidade e aceleração através de suas derivadas em função do tempo.

x = 0,04 s e n π t

x ˙ = v r e l = 0,04 π c o s π t   i ^   m / s

x ¨ = a r e l = - 0,04 π 2 s e n π t   i ^   m / s 2

Podemos também calcular a aceleração angular do mancal O através da derivada de ω .

ω = 2 s e n π t 2   k ^   r a d / s

α = π cos ⁡ π t 2   k ^ r a d / s 2

Passo 2

Beleza! Agora vamos para a resolução dos itens.

  1. A aceleração de C quando t = 3 s:

Neste instante, as variáveis valem o seguinte:

x = 0,04 s e n 3 π = 0       →   r C O = 0   i ^ + 0,2 j ^   m

x ˙ = v r e l = 0,04 π cos ⁡ 3 π = - 0,04 π   i ^   m / s

x ¨ = a r e l = - 0,04 π 2 s e n 3 π = 0   i ^   m / s 2

ω = 2 s e n 3 π 2 =   - 2 k ^   r a d / s

α = π cos ⁡ 3 π 2 = 0 k ^ r a d / s 2

Aplicando a equação da aceleração relativa nos pontos C e O:

a C = a O + α × r C O + ω × ω × r C O + 2 ω × v r e l + a r e l

Agora é só substituir valores:

a C = 0 + 0 - - 2 2 0,2 j ^ + 2 - 2 k ^ × - 0,04 π i ^ + 0

a C = - 0,297 j ^   m / s 2

Passo 3

  1. A aceleração de C quando t = ½ s:

Neste instante, as variáveis valem o seguinte:

x = 0,04 s e n π 2 = 0,04   m     →   r C O = 0,04   i ^ + 0,2 j ^   m

x ˙ = v r e l = 0,04 π cos ⁡ π 2 = 0

x ¨ = a r e l = - 0,04 π 2 s e n π 2 = - 0,04 π 2   i ^   m / s 2

ω = 2 s e n π 4 =   2 k ^   r a d / s

α = π cos ⁡ π 4 = π 2 k ^ r a d / s 2

Aplicando a equação da aceleração relativa nos pontos C e O:

a C = a O + α × r C O + ω × ω × r C O + 2 ω × v r e l + a r e l

Agora é só substituir valores:

a C = 0 + π 2 k ^ × ( 0,04   i ^ + 0,2 j ^ ) - 2 2 0,04   i ^ + 0,2 j ^ - 0,04 π 2   i ^

a C = 0,089 j ^ - 0,444 i ^ - 0,08 i ^ - 0,4 j ^ - 0,395 i ^

a C = - 0,919 i ^ - 0 , 311 j ^   m / s 2

Resposta

  1. a C = - 0,297 j ^ m s 2
  2. a C = - 0,919 i ^ - 0 , 311 j ^   m / s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra as pás do impelidor de uma bomba centrífuga que gira com uma velocidade constante no sentido horário de 200 rpm. As partículas de fluido possuem uma velocidade absoluta cuja componente
Cada um dos dois carros A e B está viajando com uma velocidade constante de 72 km/h. Determine a velocidade e a aceleração do carro A como percebida por um observador se deslocando e girando com o car
Uma câmara de teste A é utilizada para estudar enjoo. A câmara é capaz de oscilar em torno de um eixo horizontal através de O de acordo com θ = θ 0 s e n 2 π f 1 t , e, ao mesmo tempo, possui um movim
Próximo do final de sua corrida para decolagem, o avião está girando (arfagem do nariz para cima) imediatamente antes de levantar voo. A velocidade e a aceleração da aeronave, expressas em termos do m
A fita está sendo transferida do rolo A para o rolo B. Se o rolo B gira com uma velocidade angular constante ω O , determine uma expressão para a aceleração angular α = ω ˙ do rolo A em um instante qu