Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 27
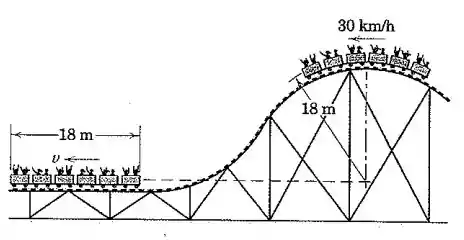
Os carros de um passeio de montanha-russa possuem uma velocidade de quando passam pelo topo do trilho circular. Despreze qualquer atrito e calcule suas velocidades quando atingem a posição horizontal na base. Na posição mais alta, o raio da trajetória circular de seus centros de massa é de , e todos os seis carros possuem a mesma massa.
Passo 1
Nesse problema, podemos utilizar a conservação da energia mecânica para calcular a velocidade . Porém, precisamos primeiro determinar qual a altura do centro de massa do sistema de carros quando passam pelo topo da montanha russa.
Então, observe a figura:
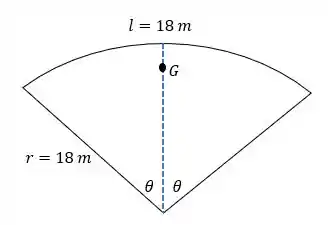
Agora, calculamos a altura do centro de massa assim:
onde é a altura de um ponto qualquer dos carros e é a massa infinitesimal. Porém, pela geometria do problema, temos:
onde é o ângulo partindo da vertical tracejada até o ponto .
Passo 2
Além disso, como a massa é distribuída uniformemente pelos carros, temos:
Mas,
Ou seja,
Passo 3
Assim sendo, obteremos:
Olhando novamente para a figura, vemos que os limites de integração serão e , onde:
Então:
Passo 4
Finalmente, usamos a equação de conservação de energia: