Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 188

Uma barra esbelta uniforme de massa M e comprimento L está em translação sobre o plano horizontal liso x - y com uma velocidade de v M quando uma partícula de massa m , que se desloca com uma velocidade v m como mostrado, atinge e se insere na barra. Determine as velocidades linear e angular final da barra com a partícula inserida.

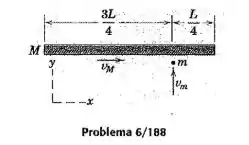
Passo 1

Pela conservação da quantidade de movimento linear, temos

G 1 x = G 2 x

De modo que

M v M = M + m v x                 ∴                 v x = M v M M + m  

Assim como

G 1 y = G 2 y

De modo que

m v m = M + m v y                 ∴                 v y = m v m M + m

Passo 2

A quantidade de movimento angular em relação ao centro de massa G do sistema logo após o impacto, quando a barra começa a rotacionar é

H G = I G × ω

Sendo que o momento de inércia de massa no centro de gravidade do sistema é dado por

I G = I - + M d 2 + m x G 2

Em que d = L / 4 - x G .

Para acharmos a localização do centro de massa x G após a colisão, fazemos

M + m x G = M L 4                 ∴                 x G = M L / 4 M + m

Assim,

I G = 1 12 M L 2 + M L 4 - M L / 4 M + m 2 + m M L / 4 M + m 2

Retomando a equação para a quantidade de movimento angular, temos

H G = I G × ω

Daí

H G = m v m M L / 4 M + m = 1 12 M L 2 + M L 4 - M L / 4 M + m 2 + m M L / 4 M + m 2 × ω

Por fim, resolvendo para ω , obtemos

ω = 12 v m L m 4 M + 7 m  

Resposta

ω = 12 v m L m 4 M + 7 m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um caixote quadrado uniformemente carregado é liberado do repouso com seu canto D diretamente acima de A; ele gira em torno de A até que seu canto B bata no chão, quando então passa a girar em torno d
Cada uma das barras AB e BC tem comprimento L = 15 pol. e peso W= 2,5 lb. Determine a velocidade angular de cada barra imediatamente após o impulso Q Δ t = ( 0.30 l b ⋅ s ) i i ser aplicado em C.
Em um jogo de sinuca, a bola A está rolando sem escorregar com uma velocidade Vo ao atingir obliquamente a bola B, que está em repouso. Denotando por r o raio de cada bola e por μ k o coeficiente de a
As barras uniformes AB e AC, cada uma com massa m e comprimento l, são parafusadas juntas em A e conectadas por pinos em pequenos roletes em B e C. Uma mola de constante k é presa aos pinos em B e C e
Uma bola de 20 g está ligada a uma raquete por meio de uma corda elástica AB de constante k = 7,5 N/m. Sabendo que a raquete é movida verticalmente de acordo com a relação δ = δ ms e nω ƒ t , ƒ com um