Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 186

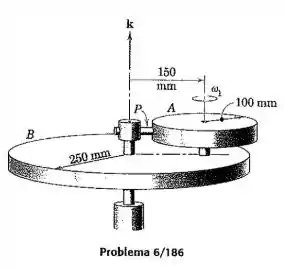
O rotor maior tem uma massa de 60   k g e um raio de giração em relação ao seu eixo vertical de 200   m m . O rotor menor é um disco circular maciço com uma massa de 8   k g e está inicialmente girando com uma velocidade angular ω 1 = 80   r a d / s com o rotor maior em repouso. Um pino acionado por mola P que gira com o rotor maior é liberado e se comprime contra a periferia do disco menor, fazendo-o parar em relação ao rotor maior. Despreze qualquer atrito no mancal e calcule a velocidade angular final do conjunto.

Passo 1

O momento de inércia de massa com relação ao ponto A é dado por

I A - = 1 2 m r 2 = 1 2 8 0,1 2 = 0,04   k g × m ²

Para B , temos

I B - = m k 2 = 10 0,2 2 = 2,4   k g × m ²

Passo 2

Inicialmente, quando só o rotor menor gira, temos

H A - = I A - ω 1 = 0,04 80 = 3,2   k g × m ² / s

Quando o rotor maior é acionado, temos

H o = I A o - I B - ω

Sendo I A o = I A - + m d ²

Inserindo os valores fornecidos no problema, temos

H o = 0,04 + 8 × 0,15 2 + 2,4 ω = 2,62 ω

Passo 3

Sabendo que o momento resultante em relação ao ponto O é nulo, temos ∆ H o = 0 . Assim,   H A - = H o . Substituindo ambas as expressões já encontradas, temos

2,62 ω = 3,2           ∴             ω = 1,221   r a d / s

Resposta

ω = 1,221   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A prancha CDE tem uma massa de 15 kg e repousa sobre um pequeno pivô em D. A ginasta A de 55 kg está de pé na prancha em C quando a ginasta B de 70 kg salta de uma altura de 2,5 polegadas e atinge o p
Resolva o problema 17. 121, assumindo que o coeficiente de restituição entre A e B é 0.8.PROBLEMA 17.121 Uma pequena placa B é presa a um cabo que é enrolado em um disco uniforme de 8 lb de raio R = 9
O membro ABC tem uma massa de 2,4 kg e está preso a um suporte de pino em B. Uma esfera D de 800 g atinge a extremidade do membro ABC com uma velocidade vertical v1 de 3 m / s. Sabendo que L = 750 mm
Uma haste delgada CDE de comprimento L e massa em está ligada a um suporte de pino em seu ponto médio D. Uma segunda haste idêntica AB está girando em torno de um suporte de pino em A com uma velocida
Uma barra delgada uniforme AB de comprimento L = 800 mm é posicionada com seu centro equidistante de dois apoios localizados a uma distância b = 200 mm entre si. A extremidade B da barra é erguida a u