Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 178
A roda de tem um diâmetro de e um raio de giração em relação ao seu eixo de . A roda carrega um eixo com , de pequeno diâmetro, através do seu centro como mostrado. Se a roda tem uma velocidade angular enquanto rola sem deslizars sobre a superfície horizontal, calcule a distância até o eixo , paralela à linha de centro do eixo, em relação a qual a quantidade de movimento angular do corpo combinado é nula.
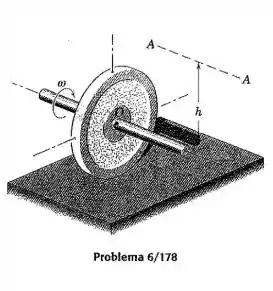
Passo 1
Se aplicarmos o Teorema dos Eixos Paralelos ao momento de inércia de massa, temos
Neste caso, temos
A velocidade do ponto , é dada por
Passo 2
Sabemos que a quantidade de movimento angular em relação ao ponto é dada por
Substituindo os valores já encontrados e os dados do problema, ficamos com
Por fim, resolvendo para :
Resposta
Exercícios de Livros Relacionados
Resolva o problema 17.123, assumindo que o impacto entre as hastes é perfeitamente elástico.17.123 - Uma haste delgada AB é liberada do repouso na posição mostrada. Ela desce para a posição vertical e
A esfera A de massa m e raio r rola sem deslizar com uma velocidade V1 em uma superfície horizontal quando atinge uma esfera idêntica B que está em repouso. Denotando por u k o coeficiente de atrito c
Resolva o problema 17. 125, assumindo que o ginasta muda de lugar de modo que o ginasta A pula na prancha enquanto Ginasta B fica em C17.125 - A prancha CDE tem uma massa de 15 kg e repousa sobre um p
Uma pequena placa B é presa a uma corda que é enrolada em volta de um disco uniforme de 4 kg e raio R = 200 mm. Um cursor A de 1,5 kg é liberado do repouso e cai de uma distância h = 300 mm antes de a
O membro ABC tem uma massa de 2,4 kg e está preso a um suporte de pino em B. Uma esfera D de 800 g atinge a extremidade do membro ABC com uma velocidade vertical v1 de 3 m / s. Sabendo que L = 750 mm