Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 29
Se o centro de gravidade das mesas empilhadas está em e a pilha pesa (), determine a menor força que o menino precisa empurrar na pilha a fim de causar um movimento. O coeficiente de atrito estático em e é . As mesas estão presas uma na outra.
Passo 1
O problema pede que descubra a menor força que consiga empurrar a pilha de mesas.
Beleza, vamos começar fazendo um diagrama de corpo livre bem simplificado, fica assim:
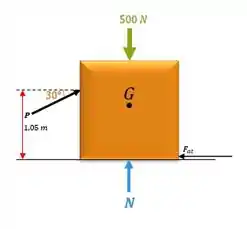
Já vamos logo começar pegando o eixo horizontal:
Passo 2
Então você já sabe como se calcula a força de atrito não sabe? A gente usa a normal multiplicado pelo coeficiênte de atrito.
Bora calcular a a normal antes:
E o atrito fica:
Passo 3
Calma, tá quase acabando, agora vamos substituir na equação do primeiro passo:
Resposta
Exercícios de Livros Relacionados
Sabendo que o coeficiente de atrito estático é 0,30 e que o tambor de freio está rodando no sentido anti-horário, determine o mínimo valor de a para o qual o freio não é autotravante.
Um cabo passa em torno de três tubos paralelos. Dois dos tubos são fixos e não podem rodar, enquanto o terceiro tubo é girado vagarosamente. Sabendo que os coeficientes de atrito são μ s = 0,25 e μ k
A velocidade de um tambor de freio mostrado na figura é controlada por uma cinta fixada a uma cinta fixada a uma barra de controle A D . A força P de intensidade de 110N é aplicada na barra de control
Um cabo passa em torno de três tubos paralelos. Sabendo que os coeficiente de atrito são μ s = 0,25 e μ k = 0,20 , determine (a) o menor peso W para o qual o equilibrio é mantido, (b) o maior peso W q
Sabendo que a = 100m m , determine o máximo valor do coeficiente de atrito estático para o qual o freio é autotravante quando o tambor roda no sentido anti-horário.