Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 71
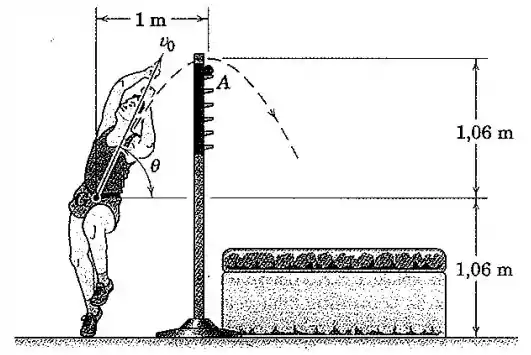
O centro de massa de um atleta de salto em altura segue a trajetória mostrada. Determine a componente , medida no plano vertical da figura, da sua velocidade de impulsão e o ângulo se o ápice da trajetória transpõe por uma margem mínima a barra em . (Em geral, o centro de massa do atleta deve ultrapassar a barra durante um salto bem-sucedido?)
Passo 1
Galera, analisando primeiramente o movimento vertical, vemos que ele ocorre com aceleração constante , e portanto podemos usar a seguinte equação:
No ponto , o ápice da trajetória, temos e , então:
Ou seja, já descobrimos qual é a componente vertical da velocidade inicial.
Passo 2
Como não há arrasto aerodinâmico, podemos considerar a velocidade horizontal constante em todo o trajeto, e portanto:
onde é o tempo de subida até o ápice. Podemos descobrir esse valor ao considerarmos a equação do movimento vertical:
Quando estamos no ápice, temos , e , conforme já calculamos no passo anterior. Então vamos substituir esses valores na equação:
Assim, obtemos a componente horizontal da velocidade inicial:
Passo 3
Show! Sabendo as duas componentes da velocidade inicial, a gente já pode descobrir o módulo da velocidade inicial e o ângulo , pois
Então,