Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 87
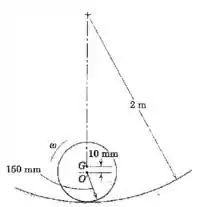
O centro de massa da roda de está deslocado do centro em . Se está na posição mostrada, com a roda rolando sem deslizar, com uma velocidade angular de , na parte mais baixa da trajetória circular com de raio, calcule a força exercida pela trajetória sobre a roda. (Tenha cuidado para utilizar a aceleração correta do centro de massa).
Passo 1
Vamos começar calculando a aceleração do centro geométrico da roda.
Podemos encontrar essa aceleração considerando que o centro mantém uma trajetória de raio , com velocidade linear :
E agora vamos calcular a aceleração do centro de massa em relação ao ponto . Isso é simplesmente a aceleração centrípeta que mantém o centro de massa em uma trajetória circular em torno de :
Passo 2
Beleza, encontramos os módulos das acelerações, mas para somá-las precisamos tratá-las como vetores, então vamos encontrar também as suas direções e sentidos.
Como ambas são acelerações centrípetas, elas devem apontar para os centros das suas respectivass trajetórias circulares.
A aceleração mantém o ponto em uma trajetória que tem centro no suporte lá em cima, portanto é vertical para cima no momento representado no desenho.
Já a aceleração mantém o centro de massa em uma trajetória que tem centro em . Olhando para o desenho, vemos que no momento que foi pedido essa aceleração é vertical para baixo.
Então:
Passo 3
Agora que sabemos a aceleração nós podemos aplicar a segunda lei de Newton na direção vertical:
E as únicas forças que atuam nessa direção são o peso e a força que queremos calcular:
Resposta
A força é .