Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 91
A roda e seu cubo possuem uma massa de , com um raio de giração em relação ao centro de . Um fio enrolado firmemente em torno de seu cubo está preso no suporte fixo, e a roda é liberada a partir do repouso sobre o plano inclinado. Se os coeficientes de atrito estático e dinâmico entre a roda e o plano inclinado são e , respectivamente, calcule a aceleração do centro da roda. Prove inicialmente que a roda desliza.
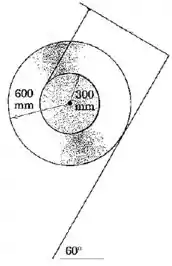
Passo 1
Primeiro queremos provar que a roda desliza. A melhor forma de fazer isso é descobrir o que seria necessário para a roda estar em equilíbrio:
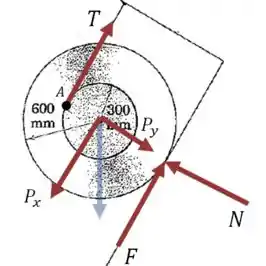
Vamos aplicar a segunda lei de Newton na direção :
E para montar uma equação de equilíbrio dos momentos, vamos tomar o ponto onde a força age, dessa forma vamos anular o seu momento, e o das forças e :
E agora que conhecemos a força de atrito e a normal , podemos calcular o coeficiente que faria a roda manter o equilíbrio:
Mas o coeficiente de atrito estático da roda com o nosso plano é apenas , ou seja, é insuficiente para manter o equilíbrio, e portanto a roda desliza.
Passo 2
Agora vamos encontrar a aceleração do centro de massa. Já que vimos que a roda desliza, vamos entrar em um regime de atrito dinâmico, e podemos calcular a força de atrito:
E aplicando a segunda lei de Newton na direção (que é a direção da aceleração que queremos encontrar):
Até aqui temos duas variáveis deconhecidas ( e ), mas apenas uma equação. Precisamos encontrar mais uma.
Passo 3
Vamos tomar a soma dos momentos em relação ao centro de massa:
Onde o momento de inércia pode ser calculado a partir do raio de giração:
E a aceleração angular do “cubo” se relaciona com a aceleração do centro de massa pela seguinte equação:
Então:
E quais são as forças que produzem momento em relação ao centro de massa? e :
Mas já conhecemos o valor de , então:
Passo 4
Agora ficamos com um sistema de duas equações:
Vamos multiplicar a segunda equação por e somar co a segunda:
Resposta
A aceleração do centro de massa é ;