Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 96
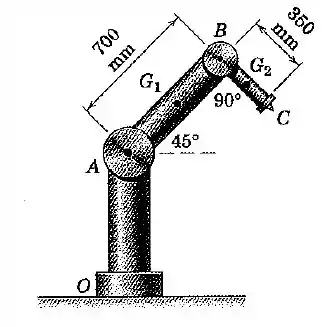
O dispositivo robótico do Prob. 6/60 é reapresentado aqui. O elemento está girando em torno da articulação com uma velocidade angular no sentido anti-horário de , e essa velocidade está aumentando a . Determine o momento exercido pelo braço sobre o braço se a articulação é mantida travada. A massa do braço é de , e o braço pode ser considerado como uma haste esbelta uniforme.
Passo 1
Vamos começar escrevendo uma equação de momentos em relação ao ponto , dessa forma o momento que queremos calcular vai aparecer na equação:
E os únicos momentos em relação ao ponto são o momento que queremos calcular e o momento da força peso:
E o primeiro termo do lado direito é fácil de escrever, pois temos o momento de inércia de uma barra esbelta em relação a um eixo na sua extremidade:
E a aceleração angular já foi dada, então:
Para escrever o último termo já teremos um pouco mais de trabalho. Pois vamos precisar conhecer cada componente da aceleração do centro de massa da barra , então teremos que calculá-lo em forma vetorial.
Passo 2
Queremos a aceleração do centro de massa da barra , que tem uma componente tangencial e uma centrípeta:
Então primeiro vamos ter que escrever o vetor posição do centro de massa da barra em relação a uma origem que vamos colocar no ponto .
Olhando o desenho já podemos escrever as componentes desse vetor:
E os vetores e apontam apenas na direção , saindo do plano da página, e os seus módulos já foram dados no enunciado:
Agora vamos resolver esse produto vetorial, escrevendo como um determinante:
Passo 3
Agora já podemos escrever o último termo daquela equação de cima, em que cada é a distância perpendicular daquela componente até o nosso ponto de referência :
Agora vamos substituir tudo na nossa equação, inclusive com os valores que calculamos lá em cima
Resposta
O momento total exercido pelo braço é .