Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 132
A carga P é abaixada pelas duas polias que estão presas uma a outra e giram como um só conjunto. Para o instante representado, o tambor A possui uma velocidade angular no sentido anti-horário de 4 rad/s, que está diminuindo em 4 rad/s a cada segundo. Simultaneamente, o tambor B possui uma velocidade angular no sentido horário de 6 rad/s, que está aumentando em 2 rad/s a cada segundo. Calcule a aceleração dos pontos C e D e a carga P.
Passo 1
Antes de começar a desenvolver, vamos evidenciar os dados da questão, pois o enunciado dá algumas informações de uma forma não muito explícita.
Agora, representar a Figura com esses dados:
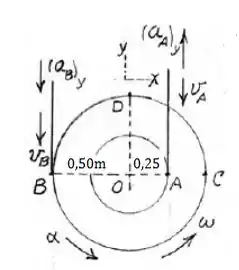
Calculando as velocidades e acelerações dos pontos A e B, temos:
Passo 2
Sabendo as velocidades e acelerações dos pontos A e B, podemos calcular a velocidade angular e a aceleração angular da polia O.
Representando apenas os vetores aceleração, temos que:
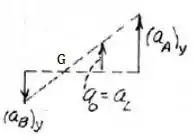
Onde a distancia dos vetores equivale a distância BA. Por semelhança, temos que:
De forma análoga, a velocidade angular pode ser dada por:
Ainda por semelhança, podemos calcular a aceleração do centro da polia O:
Então:
Passo 3
Neste passo, vamos aplicar a equação da aceleração relativa para calcular a aceleração no ponto C:
De modo análogo, calculamos a aceleração no ponto D: