Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 86
A viga de aço com possui uma massa de e é içada a partir do repouso onde a tração em cada um dos cabos é de . Se o tambores de elevação recebem acelerações angulares iniciais e , calcule as trações correspondentes e nos cabos. A viga pode ser considerada como uma barra esbelta.
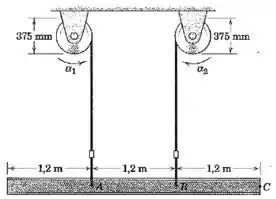
Passo 1
Vamos começar calculando as acelerações lineares associadas às acelerações angulares e nos tambores de elevação:
E essa diferença entre as duas acelerações tenderá a produzir uma rotação na barra. Podemos calcular a aceleração angular associada a esse fenômeno:
E a aceleração do centro de massa da barra será dado pela média aritmética dessas duas acelerações, já que esse centro está exatamente no ponto médio entre e :
Passo 2
Nosso objetivo é encontrar as trações e nos cabos, então vamos aplicar a segunda lei de Newton na direção vertical:
E agora vamos calcular o momento resultante em relação ao centro de massa:
O momento de inércia em relação ao centro de massa de uma barra esbelta é:
E os momentos das forças podem ser calculados com a ajuda do desenho, lembrando que a força peso terá momento nulo já que passa pelo centro de massa:
E então:
Passo 3
E assim ficamos com um sistema de duas equações:
Somando as duas equações encontramos o seguinte:
E consequentemente:
Resposta
As trações são e .