Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 182
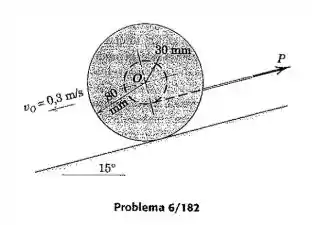
O centro da roda de com raio de giração de em relação a , tem uma velocidade para baixo na inclinação de 15° quando uma força é aplicada ao cabo enrolado em torno do seu eixo central. Se a roda rola sem deslizar, calcule a velocidade do centro quando tiver sido aplicada por cinco segundos.
Passo 1
Sabemos que a relação momento-quantidade de movimento angular é dada por
Rearranjando, encontramos
De onde tiramos que
Resolvendo a integral e colocando o raio da roda em evidência, temos
Mas sabemos também que o somatório de forças externas em x equivale à quantidade de movimento linear em x. Daí
De onde tiramos que
Passo 2
Note que chegamos a um sistema que contém duas equações e duas incógnitas
Resolvendo o sistema, obtemos
Resposta
Exercícios de Livros Relacionados
Uma bola de golfe de 46 g é golpeada com um taco de golfe e o deixa a uma velocidade de 50 m/s. Consideramos que para 0 ≤ t ≤ t 0 , onde t 0 é a duração do impacto, a intensidade F da força exercida n
O salto triplo é uma prova do atletismo em que o atleta faz uma corrida de arrancada e tenta se projetar o mais longe possível com um salto inicial, dois passos e um salto final. A figura mostra o sal
O projeto para uma nova prótese de quadril está sendo estudado usando um instrumento de inserção e um fêmur fixo falso. Considerando que o punção aplica uma força média de 2 kN durante um tempo de 2 m
A última parte da prova de salto triplo do atletismo é o salto final, em que o atleta faz o último salto e aterrissa em uma caixa de areia. Considerando que a velocidade de um atleta de 90 kg justamen
O seguinte modelo matemático foi sugerido para a variação na pressão dentro do diâmetro de 10 mm do cano de um rifle quando uma bala de 25 g é disparada: p t = 950M P a e - t / ( 0,16m s ) onde t é ex