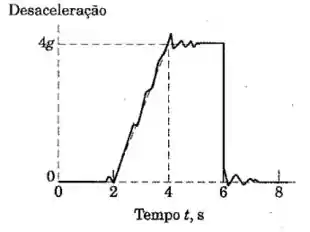
Uma força de desaceleração atua sobre uma partícula que inicialmente se desloca com uma velocidade de e fornece uma desaceleração como a registrada pela leitura do osciloscópio mostrado na figura. Determine a velocidade aproximada da partícula em e em .

Para encontrar a velocidade no instante é só substituir na equação:

E precisamos estimar a área entre os pontos e no gráfico.

Entre e nós podemos dizer que a área é nula, e que entre e o gráfico é aproximadamente uma reta. Usando a fórmula para a área do triângulo:

É importante lembra de colocar os valores com sinal negativo! Afinal de contas, o eixo representa a desaceleração. Substituindo na equação de cima:

Agora fazemos a mesma coisa para o instante :

Além da área que já calculamos, temos que considerar o trecho retangular entre e , já que o restante do intervalo tem área nula. Nesse caso:

Ou seja:

Pronto!