Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 144

O projeto para uma nova prótese de quadril está sendo estudado usando um instrumento de inserção e um fêmur fixo falso. Considerando que o punção aplica uma força média de 2 kN durante um tempo de 2 ms sobre a prótese de 200 g, determine (a) a velocidade da prótese imediatamente depois do impacto, (b) a resistência média da prótese para penetração se esta move 1 mm antes de entrar em repouso.

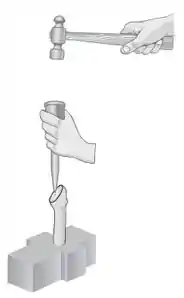
Passo 1

Que questão legal gente. Teste de resistência de próteses. Percebemos que a engenharia está em todo lugar. Para determinar a velocidade da prótese após o impacto, vamos usar o princípio de impulso e quantidade de movimento linear. Para o cálculo da resistência média da prótese, vamos usar o princípio do trabalho e energia, uma vez que a energia do impacto é transformada em trabalho da força exercida pelo punção.

Passo 2

Podemos escrever o impulso e quantidade de movimento como:

m v 1 + I m p 1 → 2 = m v 2

O impulso é calculado como:

I m p 1 → 2 = F m é d Δ t

Como a prótese parte do repouso, temos que:

0 + F m é d Δ t = m v 2

v 2 = F m é d Δ t m = 2000 ⋅ 0,002 0,200

v 2 = 20   m / s

Passo 3

O princípio de trabalho e energia é expressa por:

T 2 + U 2 - 3 = T 3

Onde o trabalho é realizado durante o movimento de penetração da prótese.

O trabalho é dado por:

U 2 → 3 = - R m é d Δ x

Assim temos:

1 2 m v 2 2 - R m é d Δ x = 0

R m é d = m v 2 2 2 Δ x = 0,200 ⋅ 20 2 2 ⋅ 0,001

R m é d = 40000   N = 40   k N

Resposta

  1. 20 m/s
  2. 40 kN
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ao supor que a força que age sobre uma bala de 2g, dentro do cano, quando atirada de um rifle varia com o tempo como mostrado no gráfico, calcular a força máxima Fo aplicada à bala no disparo, a sua v
Um bloco de 10 kg é colocado sobre o plano inclinado como mostrado na figura, as forças de 30 e 75N atuam paralelas as arestas AB e AC, respectivamente. Se ele está inicialmente em repouso, determinar
O disco tem uma massa de 15 kg. Se ele é solto do repouso quando θ = 30 ° , determine o ângulo máximo θ de repique após ele colidir com a parede. O coeficiente de restituição entre o disco e parede é
A chave de impacto consiste de uma barra fina AB de 1 kg que tem 580 mm de comprimento e pesos cilíndricos nas extremidades A e B, cada um com um diâmetro de 20 mm e massa de 1 kg. Esse conjunto está
O piloto de um avião a jato avariado foi capaz de controlar seu avião reduzindo a potência dos motres. Se o avião tem uma massa de 8500 kg e um raio de giração k G = 1,41 m em relação ao centro de mas