Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 141
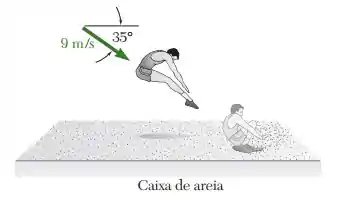
A última parte da prova de salto triplo do atletismo é o salto final, em que o atleta faz o último salto e aterrissa em uma caixa de areia. Considerando que a velocidade de um atleta de 90 kg justamente antes de aterrissar é de 9 m/s a um ângulo de 35° com a horizontal, e que o atleta para por completo em 0,22 s após a aterrissagem, determine o componente horizontal da força impulsiva média exercida sobre seus pés durante a aterrissagem.
Passo 1
Outra questão envolvendo esportes e dinâmica. Neste caso, precisamos determinar a força horizontal da força impulsiva durante a aterrissagem. Antes dos cálculos, vamos ver o diagrama de corpo livre para este movimento;
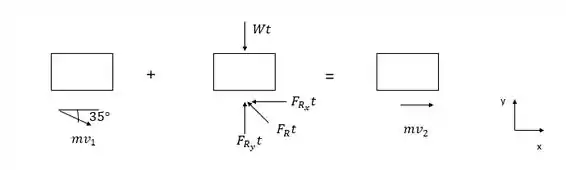
Para determinamos a componente horizontal, vamos utilizar somente as componentes horizontais do movimento.
Passo 2
Como estamos trabalhando com impulso, vamos utilizar o princípio de impulso:
Para as componentes horizontais temos: