Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 175
O centro da roda tem uma velocidade para cima na inclinação de no instante de tempo . Encontre a velocidade da roda quando . A roda tem um raio de giração de e rola sem escorregar.
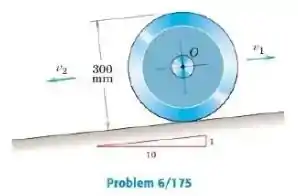
Passo 1
Seja a inclinação do plano. Segundo o enunciado, . Logo, . Sabemos que
Daí tiramos que
Passo 2
Já sabemos que a equação da quantidade de movimento angular em relação a um ponto fixo é dada por
Considerando , temos para o ponto de contato da roda com a superfície
Substituindo valores, temos
Simplificando e isolando , achamos
Resposta
Exercícios de Livros Relacionados
O bloco A tem uma massa de 40 kg e o bloco B tem uma massa de 8 kg. Os coeficientes de atrito entre todas as superfícies de contato são μ s = 0,20 e μ k = 0,15. Se P = 40 N -, determine (a) a aceleraç
Um satélite artificial de 200 kg está em órbita circular de 1.500 km sobre a superfície de Vênus. A aceleração devido à atração gravitacional em Vênus nesta altitude é 5,52 m/s2. Determine a intensida
Determine a velocidade máxima teórica que um automóvel de 2.700 lb partindo do repouso pode atingir após viajar um quarto de milha se a resistência do ar for considerada. Suponha que o coeficiente de
Cada um dos sistemas mostrados está inicialmente em repouso. Negligenciando o atrito do eixo e as massas das polias, determine para cada sistema (a) a aceleração do bloco A, (b) a velocidade do bloco
Um homem parado em um elevador que se move com uma aceleração constante, segura um bloco B de 3 kg entre dois outros blocos de tal forma que o movimento de B em relação a A e C é iminente. Sabendo que