O mecanismo mostrado se move no plano vertical. A barra vertical AB tem uma massa de 4,5 kg, e cada uma das duas hastes tem uma massa de 2,7kg com centro de massa em G e com um raio de giração de 250 mm em relação ao seu mancal (O ou C). A mola tem uma rigidez de 220 N/m e um comprimento sem deformação de 450 mm. Se o apoio D é subitamente retirado, determine a aceleração angular inicial das hastes.
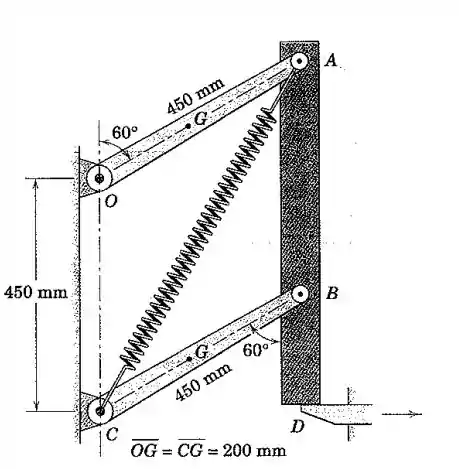
Passo 1
Bom galera, vamos considerar um deslocamento infinitesimal das hastes após a retirada do apoio. Outra coisa, vamos representar o mecanismo preenchendo com os ângulos.
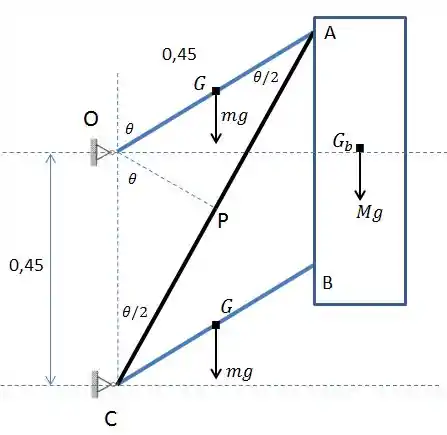
Após o deslocamento , a mola terá o seguinte comprimento (ver o triângulo OPC + OPA):
Como o enunciado diz que o comprimento natural da mola é de 0,45m, então ela possui uma deflexão de:
E seu diferencial é dado por:
Agora vamos para o calculo das energias.
A variação infinitesimal da energia potencial gravitacional pode ser escrita por:
A variação da energia potencial elástica é dada por:
A energia cinética vai ser composta pela rotação das hastes e pela translação da barra vertical. A velocidade absoluta da barra pode ser escrita pela seguinte relação com a velocidade angular das hastes:
Seu valor infinitesimal fica:
Bom, a equação da variação infinitesimal da energia cinética será composta então por (lembrando que são 2 hastes):
Onde o momento de inercia de uma haste em relação a sua extremidade é dado por:
e ainda que temos as relação:
Substituindo estes valores na equação da variação infinitesimal da energia cinética:
Bom, agora por conservação de energia temos que a soma das variações infinitesimais (1), (2) e (3) deve ser nula.
Considerando que a variação de é muito pequena, então o ângulo pode ser aproximado no seno e cosseno para o ângulo da posição inicial, isto é,
Então: