Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 74
A barra esbelta uniforme de massa e comprimento é liberada a partir do repouso na posição vertical e gira sobre sua extremidade plana em torno da quina em . (a) Se a barra desliza quando , determine o coeficiente de atrito estático entre a barra e a quina. (b) Se a extremidade da barra posui um entalhe de modo a não poder deslizar, determine o ângulo no qual o contato entre a barra e a quina termina.
Passo 1
Vamos começar definindo uma direção normal e uma tangencial, e representando as forças que atuam sobre a barra:
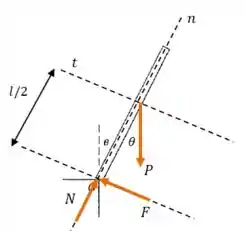
Agora podemos aplicar a segunda lei de Newton em cada direção para encontrar essas forças:
E na direção tangencial:
Passo 2
(a) Se a barra desliza quando , podemos afirmar que, nesse ponto:
Portanto:
E então precisamos calcular e para podermos encontrar .
Vamos começar calculando :
A única força que produz momento em relação ao ponto é a componente perpendicular do peso:
Passo 3
E agora que temos , podemos encontrar através da seguinte relação:
Vamos substituir e integrar:
Agora vamos substituir tudo isso na expressão que escrevemos lá em cima com :
Passo 4
(b) No ponto em que o contato entre a barra e a quina termina temos . Vamos voltar para a expressão que escrevemos antes:
E agora vamos substituir com a expressão que encontramos para :
Resposta
(a) .
(b) .