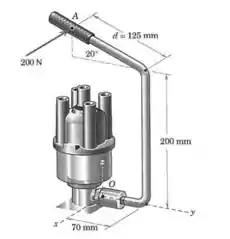
A chave especial mostrada na figura é projetada para ter acesso ao parafuso de segurança de alguns distribuidores de automóvel. Para a configuração mostrada, onde a chave está em um plano vertical e uma força horizontal de é aplicada em , perpendicular ao cabo, calcule o momento aplicado ao parafuso em . Para que valor da distância o componente de será zero?

E agora vamos calcular o produto vetorial para encontrar o momento da força:

E aplicamosa a propriedade distributiva:

Podemos usar a regra da mão direita para identificar o resultado desses produtos vetoriais (quando o produto pode ser escrito dessa forma é mais fácil do que usar o determinante!).

Então:

Agora queremos manipular o valor de para fazer com que a componente do momento seja zero.

Vamos simplesmente olhar para o cálculo que fizemos acima, e ver como chegamos naquele valor para a componente do momento:

A componente vêm da força , que não controlamos. A única forma de ser zero é se o primeiro termo é zero.

Dê uma olhada em como chegamos nesse valor no passo , ele é a componente do vetor :