Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 104
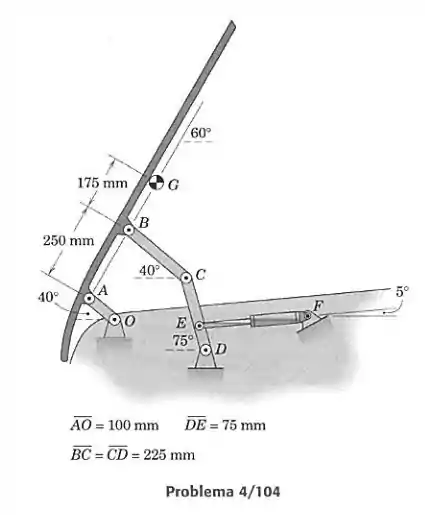
Os elementos da estrutura do capô de um carro com dobradiça frontal estão mostrados na figura. As conexões leves e e o amortecedor pressurizado mantêm o capô na posição aberta mostrada. Nesta posição, o capô está livre para girar no sentido horário em torno do pino ; o pino está travado até que o capô tenha sido abaixado a uma posição quase horizontal. Para um capô com uma massa de 40 kg, com centro de gravidade em , determine a força de compressão mínima no amortecedor que manterá a posição aberta do capô. Observe que existem duas conexões espaçadas ao longo da frente do carro, mas apenas um conjunto das outras conexões localizadas no interior do para-lama frontal direito.
Passo 1
Queremos a força que o elemento faz sobre o elemento no ponto . Coseguimos acha-la fazendo o momento em torno de ser igual a zero, mas pra isso precisamos da força causada por . Por outro lado, o capô sofre efeito das forças , e de seu peso . Então, ao resolver as equações de equilíbrio para o capô, devemos ser capazes de encontrar . Vamos representar o capô e a conexão em diagramas de corpo livre. Como as conexões são fixas nessa situação, as representaremos como parte do capô:
Passo 2
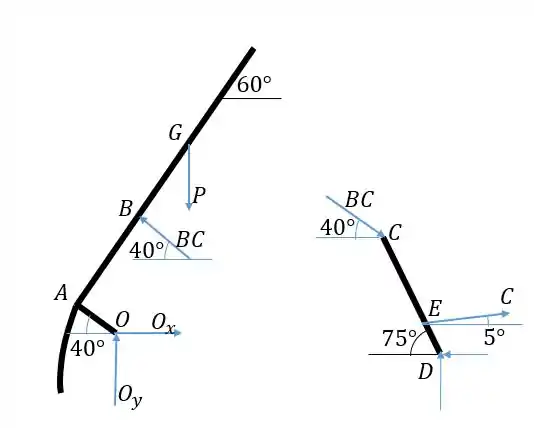
Primeiro vamos calcular , usando a soma dos momentos em torno de . Precisamos calcular as distâncias horizontal e vertical de até , e a distância horizontal de até . Primeiro para , usamos os ângulos e as distâncias dadas pelo enunciado:
Agora para :
Passo 3
Podemos então calcular o momento em torno de para achar . A força é igual a .
Passo 4
Agora olhamos para a conexão , e encontramos a força através do momento em torno de . Vamos pegar as componentes das forças que são perpendiculares ao elemento, como mostra a figura:
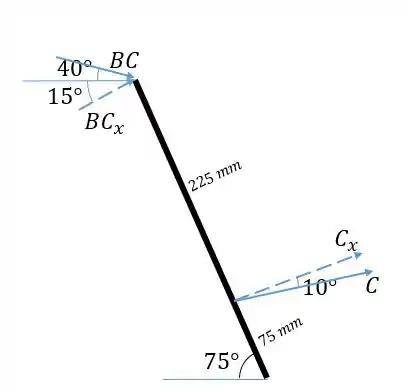
Então:
Substituindo :
O sinal negativo indica que o sentido é o contrário do que desenhamos.