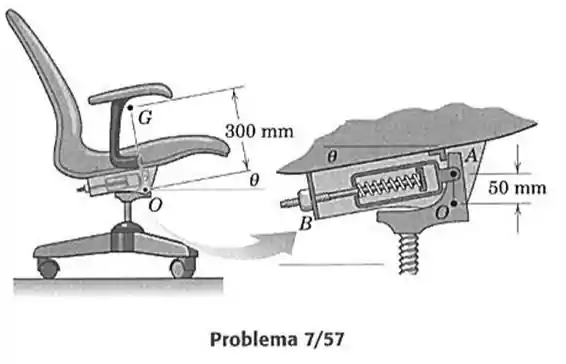
57- A figura mostra uma cadeira reclinável de escritório juntamente com um detalhe do projeto do mecanismo de inclinação suportado por uma mola. A estrutura do assento é articulada em relação ao ponto fixo na base. O aumento da distância entre e , quando a cadeira se inclina para trás em relação a , corresponde ao aumento na compressão da mola. A mola, que tem rigidez de , está sem compressão quando . Para pequenos ângulos de inclinação, pode-se assumir, com erro desprezível, que o eixo da mola permanece paralelo ao assento. O centro de massa de uma pessoa de que senta na cadeira está em , sobre uma linha perpendicular ao assento passando por . Determine o ângulo de inclinação para haver equilíbrio. (Sugestão: A deformação da mola pode ser visualizada permitindo que a base se incline do ângulo necessário em relação a , enquanto o assento é mantido em posição fixa.)
Passo 1
A energia potencial gravitacional da cadeira pode ser calculado de cardo com a seguinte imagem.
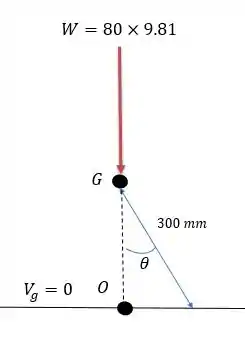
Onde a altura entre e é calculado as seguinte forma:
Onde precisa-se passar as distâncias para metros e a massa para Newtons.
Logo a energia potencial gravitacional do sistema será:
Passo 2
A sugestão nos diz que a mola ao se deformar inclina em relação a de forma que podemos aproximar a figura da seguinte forma.
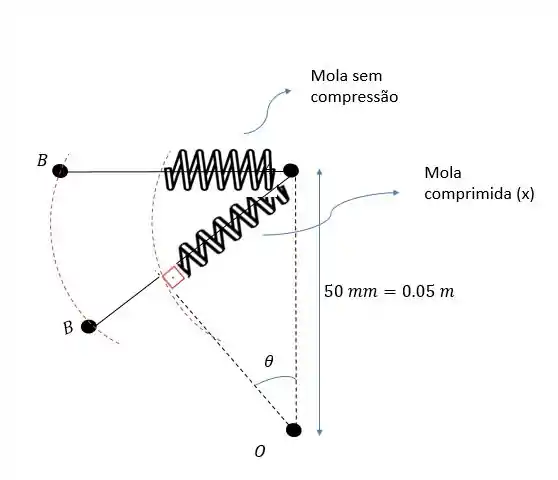
Fazendo o seno desse ângulo teremos:
Como a mola não está comprimida inicialmente então toda a compressão vale de modo que a energia potencial do sistema vale.
Já que a constante elástica vale então.
Logo toda a energia do sistema vale:
Passo 3
Para encontrar a posição de equilíbrio desse sistema devemos fazer:
Fazendo a derivada em relação ao tempo da equação da energia nós teremos:
Para essa expressão ser verdadeira ou ou
Para a primeira afirmação para a segunda:
Como queremos que a cadeira incline logo temos como resposta: