Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 119
Determine a força de compressão exercida sobre a lata para uma força aplicada quando o esmagador de latas está na posição mostrada. Note que existem duas conexões e duas , com um par de conexões de cada lado da parte fixa do esmagador. Além disso, o pino está na linha vertical central da lata. Finalmente, note que as pequenas projeções quadradas da garra móvel se deslocam nos rasgos internos da amarração fixa.
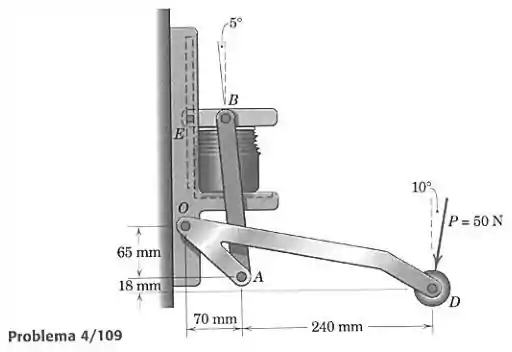
Passo 1
Vamos isolar a garra móvel e a conexão em diagramas de corpo livre, para analisar as forças atuantes sobre eles. Na garra móvel temos a força causada por , a reação em e um possível momento causado pela fixação em (já que a fixação é quadrada, impede o giro). Para a conexão , temos forças desconhecidas em a força causada por e . Consideramos como se cada par de conexões fizesse uma força só:
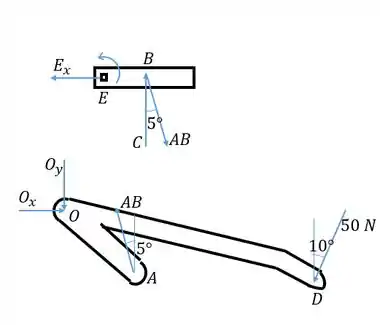
Passo 2
Primeiro, olhando para a conexão , podemos achar diretamente fazendo o momento em torno de ser zero. Usamos as distâncias dadas pelo enunciado:
Passo 3
Pela soma das forças verticais para a garra móvel: