Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 108
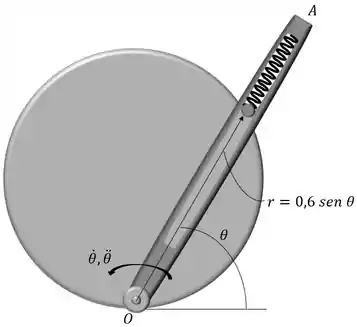
O cilindro de 1,5 kg desloca-se ao longo da trajetória descrita por m. Se o braço está girando no sentido anti-horário com uma velocidade angular de rad/s, determine a força exercida pela ranhura lisa no braço sobre o cilindro no instante . A mola tem rigidez de 100 N/m e não está deformada quando . O cilindro está em contato apenas com uma borda com ranhura. Despreze a dimensão do cilindro. O movimento ocorre no plano vertical.
Passo 1
O Problema nos deu as seguintes informações:
Massa do cilindro :
Velocidade angular: rad/s
Rigidez da mola: N/m
Movimento no plano vertical.
A questão pede para determinarmos a força exercida pela ranhura lisa sobre o cilindro quando .
Desenhamos o seguinte diagrama de corpo livre:
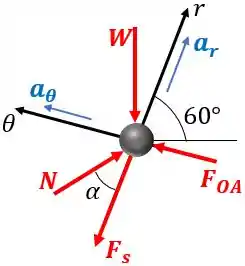
Onde é a força exercida pela ranhura do braço, é a força normal, é a força exercida pela mola sobre o cilindro e é a força peso.
Através do diagrama de corpo livre, podemos ver que o ângulo entre e o eixo é de .
Lembre-se de que a força normal é perpendicular à tangente do movimento. Como o movimento corresponde à um circulo, a direção de será a mesma do raio deste círculo.
Passo 2
Primeiramente, vamos encontrar as derivadas temporais.
Em
Para
Passo 3
Sabemos que as componentes da aceleração nas coordenadas e são dadas por
Logo,
Passo 4
Agora vamos descobrir o ângulo com que a força normal é aplicada à partícula.
Pela análise trigonométrica do seguinte triângulo, vemos que se trata de um triângulo isósceles onde e são os ângulos de base.
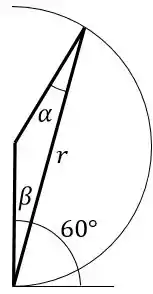
Através da imagem fornecida pelo enunciado, vemos que
Portanto, para , temos que .
Passo 5
A força elástica exercida é dada por
Onde o comprimento da mola é igual a .
O comprimento não deformado da mola é dado em . Logo,
O comprimento final da mola é igual ao valor de em . Portanto, temos que
Passo 6
Aplicaremos as Equações do Movimento.
Utilizaremos .
No eixo :
No eixo :