Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 40

O cilindro está apoiado em A , vértice de um furo cônico em sua base. Determine a distância míni m a ⁡ d a fim de que ele permaneça em equilibrio estável.

Passo 1

Primeiro, vamos desenhar o diagrama de força ativa

Uma vez que não há forças externas agindo, apenas a gravidade, podemos escrever a equação de equilíbrio como:

δ V = 0   ⇒   δ V g = 0 (1)

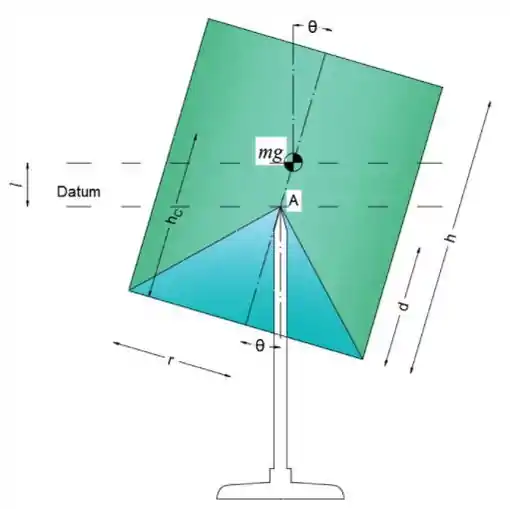
Para resolver este problema, devemos imaginar que os cilindros giram em torno do ponto A, e então verificar sua estabilidade quando estiver na posição horizontal, ou seja, em θ = 0 ^ ∘

Para determinar a diferença de altura entre o ponto A e o centro de massa, primeiro devemos determinar o centro de massa.

h C = ρ h 1 V 1 - ρ h 2 V 2 ρ V 1 - V 2

Observe que estamos nos referindo ao cilindro como objeto "1 " e ao furo cônico como objeto "2 '', portanto, tanto o centro de massas quanto os volumes devem ser fornecidos na tabela no final do livro.

h C = h 2 + r 2 π ⋅ h - d 4 ⋅ d 3 r 2 π r 2 π ⋅ h - d 3 r 2 π = h 2 2 - d 2 12 h - d 3 = 6 h 2 - d 2 12 h - 4 d

Agora podemos escrever a expressão para a diferença de altura l como:

l = h C - d c o s ⁡ θ l = 6 h 2 - d 2 12 h - 4 d - d c o s ⁡ θ l = 6 h 2 - 12 h d + 3 d 2 12 h - 4 d c o s ⁡ θ (2)

Passo 2

A expressão para energia potencial gravitacional é:

V g = m g l

Substituiremos l pela expressão (2)

V g = m g 6 h 2 - 12 h d + 3 d 2 12 h - 4 d c o s ⁡ θ

Derive ambos lados da equação para obter

δ V g = - m g 6 h 2 - 12 h d + 3 d 2 12 h - 4 d s i n ⁡ θ δ θ (2)

Substituiremos δ V g pela expressão (2) na equação do equilíbrio (1)

δ V = - m g 6 h 2 - 12 h d + 3 d 2 12 h - 4 d s i n ⁡ θ δ θ = 0

Observe que o sistema é estável quando a segunda derivada da equação de equilíbrio é maior que zero

  ( δ V ) d V d θ > 0

Substitua δ V pela expressão (1.1)

- m g 6 h 2 - 12 h d + 3 d 2 12 h - 4 d s i n ⁡ θ δ θ d V d θ > 0

Derive ambos lados da equação

- m g 6 h 2 - 12 h d + 3 d 2 12 h - 4 d c o s ⁡ θ > 0 (3)

Passo 3

Para verificar a estabilidade da posição θ = 0, vamos simplesmente colocar o valor de θ na expressão (3)

- m g 6 h 2 - 12 h d + 3 d 2 12 h - 4 d c o s ⁡ 0 > 0

Dividiremos ambos lados da equação por m g c o s ⁡ 0 12 h - 4 d ' , uma vez que a expressão é constante e positiva

- 6 h 2 + 12 h d - 3 d 2 > 0

Também podemos escrever esta não equação como:

3 d 2 - 12 h d + 6 h 2 < 0

Como isso não é uma equação, precisaremos encontrar suas raízes primeiro e, em seguida, determinar se a solução é maior ou menor que a raiz

d 1 / 2 = 12 h ± ( 12 h ) 2 - 4 ⋅ 3 ⋅ 6 h 2 2 ⋅ 3 d 1 / 2 = 12 h ± 144 h 2 - 72 h 2 2 ⋅ 3 ⇒ d 1 = 3.41 h ⇒ d 2 = 0.586 h

Como d

Vamos verificar a expressão para d = 0

f ( 0 ) = 3 ⋅ 0 2 - 12 ⋅ 0 h + 6 h 2 f ( 0 ) = 6 h 2 > 0

Como a função é positiva para d = 0, podemos concluir que será negativa para 0,586h≤d≤3,41h, e novamente positiva para d> 3,41h. Posto isto, podemos dizer que a distância mínima d para que o cilindro fique estável é:

d = 0.586 h

Resposta

d = 0.586 h

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

35- A energia potencial de um sistema mecânico é dada por V = 6 x 3 - 9 x 2 + 7 , onde x é a coordenada de posição associada ao único grau de liberdade. Determine a posição, ou as posições, de equilíb
Uma mola com rigidez à torção k está presa à articulação em B . Ela não está deformada quandoo conjunto de hastes está na posição vertical. Determine o peso W do bloco que resulta em equilíbrio neutro
Se a haste uniforme O A tem massa de 12k g , determine a massa m que a manterá em equilibrio quando θ = 30 ∘ . O ponto C coincide c o m ⁡ B quando OA está na horizontal. Despreze o tamanho da polia em
Se a mola tem rigidez à torsão k = 300N ⋅ m / r a d e não está deformada quando θ = 90 ∘ , determine o ângulo de equilibrio se a esfera tem massa de 20k g . Investigue a estabilidade nessa posição. A