Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 42
Se a haste uniforme tem massa de , determine a massa que a manterá em equilibrio quando ponto coincide quando OA está na horizontal. Despreze o tamanho da polia em .
Passo 1
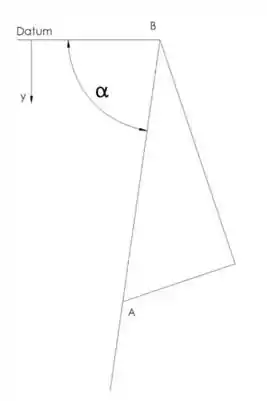
Datum é colocado na junta. Para calcular todas as distâncias a partir do datum, primeiro vamos introduzir um ângulo adicional α. Este ângulo representará o ângulo da haste AB e datum como mostrado na imagem. A soma dos ângulos θ e ϕ é constante. Agora vamos calcular a função potencial:
Para cálculos adicionais, precisaremos calcular ângulos constantes:
Passo 2
Agora vamos calcular a derivada da função potencial:
Passo 3
Resposta
Exercícios de Livros Relacionados
Se a função de potencial de um sistema conservativo com um grau de liberdade é V = ( 10 cos 2 θ + 25 sin θ ) J , onde 0 °θ180 ° , determine as posições de equilíbrio e investigue a estabilida
A pequena balança postal consiste em um contrapeso W 1 , conectado aos elementos que possuem peso desprezível. Determine o peso W 2 que está na bandeja em termos dos ângulos θ e ϕ e das dimensões most
A haste uniforme A D tem 20k g de massa. Se a mola conectada não está deformada quando θ = 90 ° , determine o ângulo θ para haver equilíbrio. Observe que a mola sempre permanece na posição vertical, e
Cada elemento tem uma massa por comprimento m 0 . Determine os ângulos θ e ϕ nos quais eles estão suspensos em equilíbrio. O contato em A é liso, e ambos são conectados por um pino em B .
Determine o ângulo θ para haver equilíbrio e investigue a estabilidade nessa posição. As hastes possuem massa de 3k g cada uma e o bloco suspenso D tem massa de 7k g . A corda D C tem comprimento tota