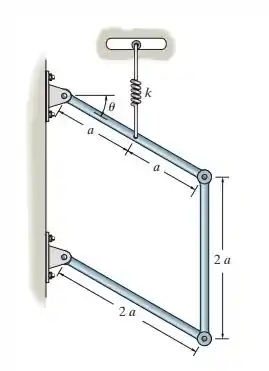
Se cada um dos três elementos do mecanismo tem peso , determine o ângulo de equilíbrio. A mola, que sempre permanece na vertical, não está deformada quando .
Passo 1
Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.
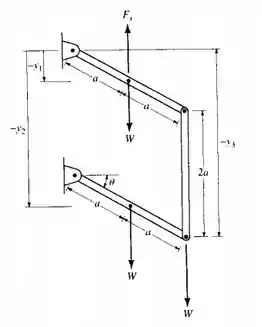
Este problema nos pede para determinarmos o ângulo . Primeiro, vamos esboçar o DCL:
Passo 2
Em seguida, temos que a posição dos pontos , e são medidos a partir do ponto fixo, usando coordenadas de posição , e , respectivamente. Pelo deslocamento virtual, temos:
Passo 3
Agora, vamos ulizar relação do trabalho virtual, temos:
Substituindo as equações que encontramos no passo anterior, temos:
Com isso, assumindo que , temos que . Logo:
Assim, vai ser:
É isso, galera, Bora resolver mais questões pra ficar craque.