Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 41
Se a mola tem rigidez à torsão e não está deformada quando , determine o ângulo de equilibrio se a esfera tem massa de . Investigue a estabilidade nessa posição. A luva pode deslizar livremente ao longo da guia vertical. Despreze o peso das hastes e da luva .
Passo 1
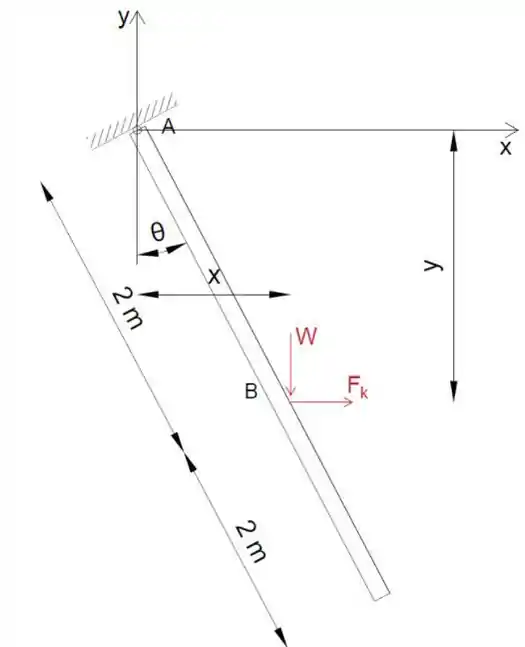
As coordenadas do ponto onde a viga repousa na mola são x e y.
E
A tarefa é dada que a massa é m = 100 kg, então o peso W será:
Passo 2
Força no ponto é:
Para que haja equilíbrio, a primeira derivada da força de cisalhamento em um ângulo deve ser igual a zero.
Calculando a equação, obtemos que o ângulo:
Resposta
Exercícios de Livros Relacionados
A haste uniforme tem massa de 100k g . Se a mola não estiver deformada quando θ = 60 ° , determine o ângulo θ para haver equilíbrio e investigue a estabilidade na posição de equilíbrio. A mola sempre
O bloco triangular de peso W se apoia sobre os cantos lisos que estão separados por uma distância a . Se o bloco possui três lados iguais de comprimento d , determine o ângulo θ para que haja equilíbr
As duas hastes possuem massa de 8k g cada. Determine a rigidez k exigida para a mola, de modo que haja equilíbrio quando θ = 60 ° . A mola tem comprimento de 1m quando não deformada. Investigue a esta
Determinar o ângulo θ para haver equilíbrio e investigar a estabilidade nessa posição. As hastes possuem massa de 10k g cada e a mola tem comprimento não deformado de 100m m .
Se cada um dos três elementos do mecanismo tem peso W , determine o ângulo θ de equilíbrio. A mola, que sempre permanece na vertical, não está deformada quando θ = 0 ° .