Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 30

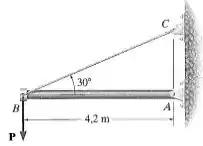
30. O tubo de aço A - 36 tem diâmetro externo de   50   m m . Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5   m m , o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima P   =   20   k N sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos.

Passo 1

Primeiro, vamos montar o diagrama de forças para o ponto B :

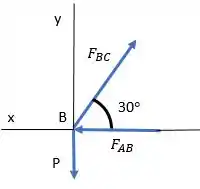
E fazer o somatório de momentos:

↶ + ∑ M A = 0 → 4,2   m × 20   k N - F B C s e n 30 ° × 4,2   m = 0

F B C = 4,2   m × 20   k N 4,2   m × s e n ( 30 ° )

F B C = 40   k N

Temos também que:

P c r = 40   k N ⋅ c o s ⁡ ( 30 ° )

Porque F B C é a força que age na haste

P c r = 40   k N ⋅ 3 2

∴ P c r = 34,64   k N

Passo 2

Conhecida as forças em ambas hastes, vamos calcular primeiro a carga máxima para que não haja flambagem na haste A B e depois para a haste B C .

P c r = π 2 E I ( k L ) 2

Como as extremidades estão presas por pinos, temos k = 1 .

O momento de inércia de uma seção circular, é dado pela fórmula:

I = π 4 r 4

Mas a haste tem um furo no meio a nova fórmula de momento de inércia será:

I = π 4 ( r e 4 - r i 4 )

Onde r i é o raio interno, r e é o raio externo.

E temos, também, por ser dado no enunciado que é um aço A - 36 :

E = 200 × 10 9   P a

P c r = π 2 ( 200 × 10 9   P a ) ( π 4 0,025 4 - r i 4   m 4 ) ( 1 × 4,2   m ) 2

P c r = F A B = 34,64   k N

34,64   k N = π 2 ( 200 × 10 9   P a ) ( π 4 0,025 4 - r i 4   m 4 ) ( 1 × 4,2   m ) 2

r i 4 = π 4 0,025 4 - 34,64   k N × ( 1 × 4,2   m ) 2 π 2 200 × 10 9   P a   m 4

r i = 20,53   m m

d i = 2 ⋅ r i = 2 ⋅ 20,53   m m

d i = 41,07   m m ≅ 40   m m

Passo 3

Vamos calcular a tensão devido à força crítica σ c r para verificar se ele ultrapassa a tensão de escoamento σ e :

σ c r = P c r A

σ c r = 34,64   k N π × ( 0,0 275 2 - 0,0 2 2 )   m 2

∴ σ c r = 30,95   M P a

σ c r = 30,95   M P a < σ e = 250   M P a

Como σ c r < σ e , a carga crítica é admissível elemento.

Resposta

O diâmetro interno necessário para que não haja flambagem na haste com a carga aplicada:

d i = 41,07   m m ≅ 40   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um perfil de aço laminado W200 x 46,1 é usado para formar uma coluna com comprimento de flambagem de 6,4 m. Usando o método da tensão admissível, determine a força centrada admissível se a tensão de e
Um tubo estrutural com a seção transversal retangular mostrada é utilizado como coluna com comprimento de flambagem de 5m. Sabendo que σ Y = 250M P aeE = 200G P a , utilize o método das tensões admiss
Uma coluna de comprimento flambagem de 4,6m deve suportar uma força centrada de 525k N . Usando o método de tensão admissível selecione o perfil de mesa larga de 200m m de altura nominal que deve ser
Duas cantoneiras de 89m m×64m m são soldadas ​​como mostra a figura, para formarem uma coluna de flambagem de 2,4m para suportar uma força centrada de 180k N . Sabendo que as cantoneiras disponíveis t
Uma coluna de comprimento flambagem de 685,8m m deve suportar uma força centrada central de 1821k N . Usando o método de tensão admissível selecione o perfil de mesa larga de 360m m de altura nominal