Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 57

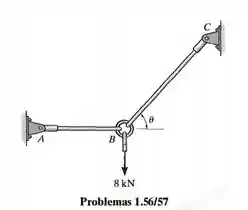
Os diâmetros das hastes A B e B C são 4   m m e 6   m m , respectivamente. Se a carga vertical de 8   k N for aplicada ao anel em B , determine o ângulo θ da haste B C de modo que a tensão normal média em cada haste seja equivalente. Qual é essa tensão?

Passo 1

Fala aí galerinha do responde aí, tudo de boa?

Vamos fazer um diagrama de corpo livre para entender o que está acontecendo:

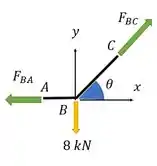
Dizer que a tensão média em cada haste é equivalente é dizer que

σ B A m e d = σ B C m e d

Mas lembrando da expressão de tensão média numa haste de seção circular

σ m e d = F π 4 d 2

Queremos que:

F B A π 4 d B A 2 = F B C π 4 d B C 2 ∴ F B A d B A 2 = F B C d B C 2

Esses diâmetros já temos. Precisamos então achar F B A e F B C . Bora!

Passo 2

Podemos olhar para o nosso DCL assim:

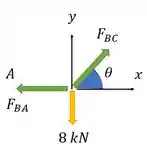
Como esse sistema está em equilíbrio, o somatório de forças em y e em x   zera. Aí podemos escrever:

∑ F y = 0

F B C   s e n θ = 8 ⋅ 10 3   N

F B C = 8 s e n θ

∑ F x = 0

F B C   c o s θ = F A B

F B A = F B C cos ⁡ θ = 8 ⋅ 10 3  cos ⁡ θ s e n θ

Repara que achamos expressões para as nossas F ’s! Podemos partir para o próximo passo.

Passo 3

Voltando lá para a nossa igualdade de tensões médias:

F B A d B A 2 = F B C d B C 2

Substituindo os diâmetros e as nossas forças:

F B C = 8 ⋅ 10 3 s e n θ

F B A = 8 ⋅ 10 3 cos ⁡ θ s e n θ

d B A = 4   m m = 0,004   m

d B C = 6   m m = 0,006   m

∴

8 ⋅ 10 3 cos ⁡ θ s e n θ   0,004 2 = 8 ⋅ 10 3 s e n θ   0,006 2

Resolvendo para θ temos que:

8 × 10 3 cos ⁡ θ 0,004 2 = 8 × 10 3 0,006 2

cos ⁡ θ = 0,004 2 0,006 2 = 0,444

θ = 63,61 °

Agora, basta calcular a tensão:

F B C = 8 ⋅ 10 3 s e n 63,61 = 8,93 k N

σ = F B C π 4 d B C 2 = 8,93 k N π 4 × 6 m m 2

σ = 315,85   M P a

Resposta

θ = 63,61 °

σ = 315,85   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os diâmetros das hastes A B e B C são 4m m e 6m m , respectivamente. Se for aplicada uma carga de 8k N ao anel em B , determine a tensão normal média em cada haste se θ=60 ° .
Cada uma das barras da treliça tem área de seção transversal de 780 m m ² ². Se a tensão normal média máxima em qualquer barra não pode ultrapassar 140M P a , determine o valor máximo P das cargas que
Cada uma das barras da treliça tem área de seção transversal de 780mm². Determine a tensão normal média em cada elemento resultante da aplicação da carga P = 40 kN. Indique se a tensão é de tração ou
O gancho é usado para sustentar o tubo de tal modo que a força no parafuso vertical é 775N . Determine a tensão normal média desenvolvida no parafuso B C se ele tiver diâmetro de 8m m . Considere que
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,84 MPa, determine a maior carga vertical P aplicada no centro que ele pode suporta